Trên đồ thị hs y = 2x-5/ 3x-1 có bao nhiêu điểm có toạ độ là các số nguyên?
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Chọn C
Tập xác định ![]()
Ta có ![]()
![]()
![]()
Ta có ![]() nên
nên ![]()
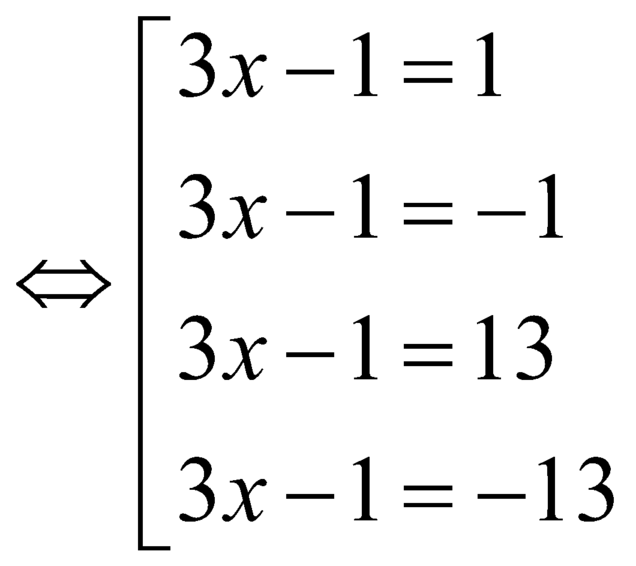
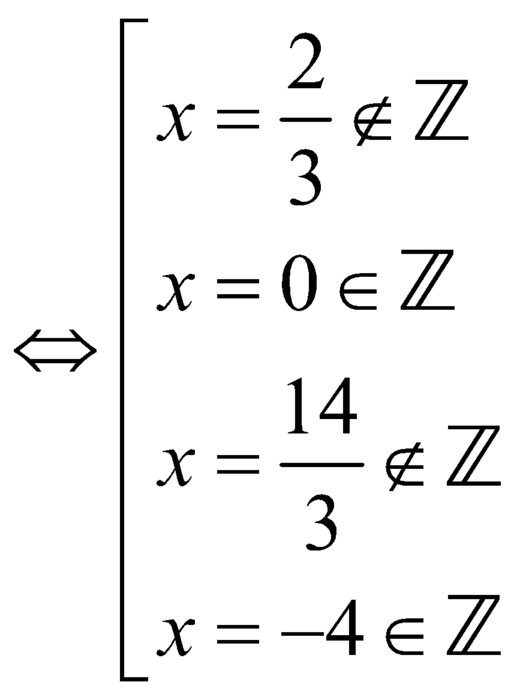 .
.
Thử lại ![]() và
và ![]() thỏa mãn.
thỏa mãn.
Vậy có hai điểm có tọa độ nguyên ![]() và
và ![]() .
.

Đáp án C
Có 2 điểm có tọa độ nguyên thuộc ĐTHS là A 0 ; 5 , B − 4 ; 1 .

b: Tọa độ giao điểm là:
\(\left\{{}\begin{matrix}3x^2-2x-1=0\\y=3x^2\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}3x^2-3x+x-1=0\\y=3x^2\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}\left(x-1\right)\left(3x+1\right)=0\\y=3x^2\end{matrix}\right.\Leftrightarrow\left(x,y\right)\in\left\{\left(1;3\right);\left(-\dfrac{1}{3};\dfrac{1}{3}\right)\right\}\)

Chọn B
Ta có: ![]() . Gọi
. Gọi ![]() suy ra
suy ra ![]() , ta có
, ta có ![]()
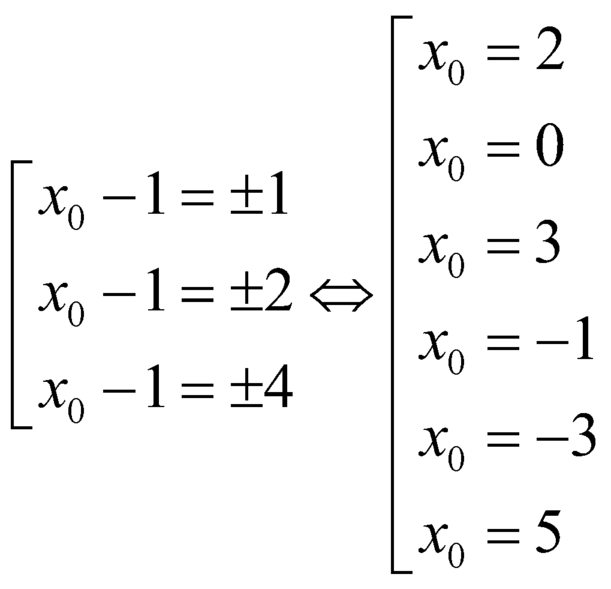 . Vậy có
. Vậy có ![]() điểm có tọa độ nguyên.
điểm có tọa độ nguyên.

Tọa độ giao điểm là:
3/2x-2=-1/2x+2 và y=-1/2x+2
=>2x=4 và y=-1/2x+2
=>x=2 và y=-1+2=1
có `y=f(x)=3/2x-2`
`y=g(x)-1/2x+2`
2 đồ thị hàm số cắt nhau tại tọa độ có phương trình
`f(x)=g(x)`
`<=>3/2x-2=-1/2x+2`
`<=>3/2x+1/2x=2+2`
`<=>2x=4`
`<=>x=2`
`=>y=3/2*2-2=1`
Vậy 2 đồ thị hàm số cắt nhau tại tọa độ (2;1)


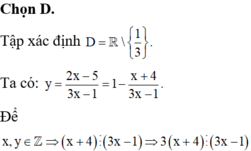

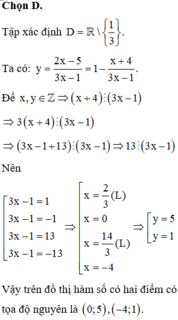
\(y=\dfrac{2x-5}{3x-1}\in Z\Rightarrow\dfrac{3\left(2x-5\right)}{3x-1}\in Z\)
\(\Rightarrow\dfrac{6x-15}{3x-1}\in Z\Rightarrow2-\dfrac{13}{3x-1}\in Z\)
\(\Rightarrow13⋮3x-1\Rightarrow3x-1=\left\{-13;-1;1;13\right\}\)
\(\Rightarrow x=\left\{-4;0\right\}\)
Có 2 điểm có tọa độ nguyên