Cho hình chóp S. ABCD có thể tích V . Gọi M, N lần lượt là trung điểm SA , MC. Thể tích của khối chóp N.ABCD là?
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
CM
4 tháng 8 2017
Đáp án B
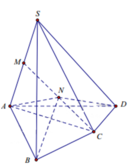
Vì N C = M N và M A = M S nên d N ; A B C D = 1 2 d M ; A B C D
Thể tích khối chóp N.ABCD là: V = 1 3 d N ; A B C D . S A B C D = 1 4 . 1 3 d S ; A B C D . S A B C D = V 4
CM
18 tháng 2 2017
Đáp án D
Hướng dẫn giải:
Ta có S A B C = a 2 2 , S A = S B 2 - A B 2 = a 3
V S . A B C = 1 3 S A . S A B C = 1 3 a 3 . a 2 2 = a 3 3 6
Ta lại có V B . N A M V B . C A S = B N B C . B M B S = 1 4
⇒ V B . N A M = 1 4 V B . C A S
Kết luận V A . S C N M = V S . A B C - V B . N A M = a 3 3 8
CM
22 tháng 1 2018
Đáp án C
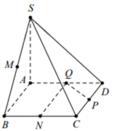
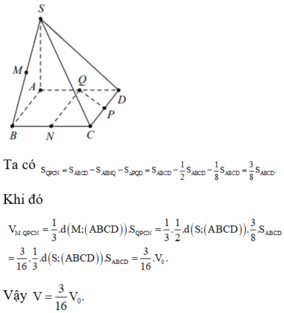
Ta có
S Q P C N = S A B C D − S A B N Q − S Δ P Q D = S A B C D − 1 2 S A B C D − 1 8 S A B C D = 3 8 S A B C D .
Khi đó
V M . Q P C N = 1 3 . d M ; A B C D . S Q P C N = 1 3 . 1 2 . d S ; A B C D . 3 8 . S A B C D = 3 16 . 1 3 . d S ; A B C D . S A B C D = 3 16 . V 0 .
Vậy V = 3 16 V 0 .
CM
7 tháng 10 2017
Chọn C
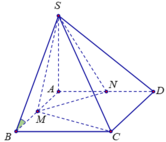
nên góc giữa mặt phẳng (SBC) và (ABCD) là . Do đó SA = AB tan450 = a
Mặt khác:
Vậy:
CM
1 tháng 9 2017
Chọn B.
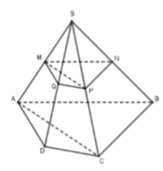
Phương pháp
Sử dụng công thức tính tỉ số thể tích đối với khối chóp tam giác
Chú ý: Công thức tỉ số thể tích trên chỉ áp dụng đối với chóp tam giác.
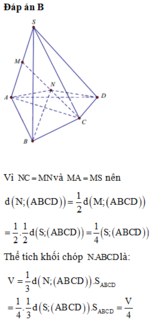
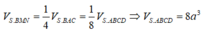
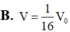
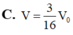
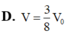
M là trung điểm SA \(\Rightarrow d\left(M;\left(ABCD\right)\right)=\dfrac{1}{2}d\left(S;\left(ABCD\right)\right)\)
N là trung điểm MC \(\Rightarrow d\left(N;\left(ABCD\right)\right)=\dfrac{1}{2}d\left(M;\left(ABCD\right)\right)=\dfrac{1}{4}d\left(S;\left(ABCD\right)\right)\)
\(\Rightarrow V_{NABCD}=\dfrac{V}{4}\)