1. Có 3 hộp đựng bi. Hộp một có 3 viên bi đỏ, hộp hai có 2 viên bi đỏ và 3 viên bi xanh, hộp ba có 4 viên bi đỏ và 1 viên bi xanh. Lấy ngẫu nhiên từ hộp một và hộp hai ra mỗi hộp 1 viên bi rồi bỏ...

VT

Vĩnh Tran

31 tháng 8 2021

1. Có 3 hộp đựng bi. Hộp một có 3 viên bi đỏ, hộp hai có 2 viên bi đỏ và 3 viên bi xanh, hộp ba có 4 viên bi đỏ và 1 viên bi xanh. Lấy ngẫu nhiên từ hộp một và hộp hai ra mỗi hộp 1 viên bi rồi bỏ vào hộp ba, sau đó từ hộp ba lấy ngẫu nhiên ra 1 viên bi thì được bi đỏ. Tính xác suất để viên bi lấy được là của hộp...

Đọc tiếp

#Toán lớp 11

0

HT

Huỳnh Trang

7 tháng 9 2021

Có3hộpđựngbi.Hộpmộtcó3viênbiđỏ,hộphaicó2viênbiđỏvà3viênbi xanh, hộp ba có 4 viên bi đỏ và 1 viên bi xanh. Lấy ngẫu nhiên từ hộp một và hộp hai ra mỗi hộp 1 viên bi rồi bỏ vào hộp ba, sau đó từ hộp ba lấy ngẫu nhiên ra 1 viên bi thì được bi đỏ. Tính xác suất để viên bi lấy được là của hộp ba.

#Toán lớp 11

1

HN

Huy Nguyễn

13 tháng 3 2022

có một hộp viên bi xanh 1 viên bi đỏ 1 viên bi vàng và 1 viên bi có kích thước và khối lượng như nhau mỗi lần An lấy một viên bi ra và ghi lại một 1 viên bi sau đó lại bỏ bi vào hộp sau 30 lần liên tiếp lấy bi có 9 lần xuất hiện bi màu đỏ , 10 lần xuất hiện bi màu vàng Tính xác suất trực nghiệm xuất hiện bi màu xanh

Đúng(0)

BT

Bùi Thanh Tùng

11 tháng 12 2015 - olm

Có 2 hộp bi. Hộp thứ nhất có 10 viên trong đó có 1 viên bi đỏ và 9 viên bi xanh. Hộp thứ hai có 8 viên bi xanh và 2 viên bi đỏ. Lấy ngẫu nhiên 1 viên bi từ hộp thứ nhất bỏ sang hộp thứ hai, sau đó lấy ngẫu nhiên 2 viên từ hộp thứ hai. Tính xác suất để:
a, Cả 2 viên bi lấy được đều là đỏ.

b, Trong 2 viên bi được lấy có 1 viên bi đỏ và 1 viên bi xanh.

#Toán lớp 9

0

PT

Pham Trong Bach

9 tháng 4 2017

Hộp A có 4 viên bi trắng, 5 viên bi đỏ và 6 viên bi xanh. Hộp B có 7 viên bi trắng, 6 viên bi đỏ và 5 viên bi xanh. Lấy ngẫu nhiên mỗi hộp một viên bi, tính xác suất để hai viên bi được lấy ra có cùng màu A. 44 135 B. 88 135 C. 45 88 D. 91 135 ...

Đọc tiếp

#Toán lớp 11

1

CM

Cao Minh Tâm

9 tháng 4 2017

Chọn A

Lời giải

Không gian mẫu là số sách chọn ngẫu nhiên mỗi hộp 1 viên bi

Số phần tử của không gian mẫu là Ω = C 15 1 . C 18 1

Gọi X là biến cố "2 viên bi lấy ra từ mỗi hộp có cùng màu"

Ta có các kết quả thuận lợi cho biến cố X như sau

● Hộp A lấy ra 1 bi trắng và hộp B lấy ra 1 bi trắng, có C 4 1 . C 7 1 cách

● Hộp A lấy ra 1 bi đỏ và hộp B lấy ra 1 bi đỏ, có C 5 1 . C 6 1 cách

● Hộp A lấy ra 1 bi xanh và hộp B lấy ra 1 bi xanh, có C 6 1 . C 5 1 cách

Suy ra số phần tử của biến cố

Vậy xác suất cần tính

P ( X ) = Ω x Ω = 44 135

Đúng(0)

MM

^-^MFF☆Vũ minh☆MFF^-^(*•.¸♡❤๖ۣۜţęąm...

10 tháng 7 2021 - olm

Có 5 hộp đựng bi xanh và bi đỏ được đánh dấu thứ tự là 1, 2, 3, 4 ,5. Hộp 1 có 29 viên bi, hộp 2 có 31 viên bi, hộp 3 có. 32 viên bi, hộp 4 có 35 viên bi, hộp 5 có 37 viên. Lấy ngẫu nhiên ra một hộp và nhận thấy rằng ở bốn hộp còn lại có số viên bi xanh nhiều gấp 3 lần số viên bi đỏ. Hỏi hộp được lấy ra là hộp số...

Đọc tiếp

#Toán lớp 5

2

A

꧁༺ác๖ۣۜmộng๖ۣۜтєαм๖ۣۜвóиɢ๖ۣۜđêм๖ۣۜт...

10 tháng 7 2021

câu hỏi giài thế

Đúng(0)

NL

Nguyễn Lan Chi

10 tháng 7 2021

Hộp số 3

Đúng(0)

PT

Pham Trong Bach

7 tháng 12 2018

Một hộp đựng 9 viên bi trong đó có 4 viên bi đỏ và 5 viên bi xanh. Lấy ngẫu nhiên từ hộp 3 viên bi. Tìm xác suất để 3 viên bi lấy ra có ít nhất 2 viên bi màu xanh.

A. 10 11

B. 5 14

C. 25 42

D. 5 42

#Mẫu giáo

1

CM

Cao Minh Tâm

7 tháng 12 2018

Đáp án là C

Đúng(0)

PT

Pham Trong Bach

3 tháng 11 2019

Một hộp đựng 9 viên bi trong đó có 4 viên bi đỏ và 5 viên bi xanh. Lấy ngẫu nhiên từ hộp 3 viên bi. Tìm xác suất để 3 viên bi lấy ra có ít nhất 2 viên bi màu xanh.

A. 10 11

B. 5 14

C. 25 42

D. 5 42

#Mẫu giáo

1

CM

Cao Minh Tâm

3 tháng 11 2019

Đáp án C

Để xác định biến cố, ta xét các trường hợp sau:

+) 2 bi xanh và 1 bi đỏ, suy ra có C 5 2 . C 4 1 = 40 cách.

+) 3 bi xanh và 0 bi đỏ, suy ra có C 5 3 = 10 cách.

Suy ra xác suất cần tính là P = 40 + 10 C 9 3 = 25 42

Đúng(0)

QT

Quoc Tran Anh Le

Giáo viên

27 tháng 9 2023

Hộp thứ nhất chứa 4 viên bi xanh, 3 viên bi đỏ. Hộp thứ hai chứa 5 viên bi xanh, 2 viên bi đỏ. Các viên bi có kích thước và khối lượng như nhau. Lấy ra ngẫu nhiên từ mỗi hộp 2 viên bi. Tính xác suất của mỗi biến cố sau:a) “Bốn viên bi lấy ra có cùng màu”b) “Trong 4 viên bi lấy ra có đúng 1 viên bi xanh”c) “Trong 4 viên bi lấy ra có đủ cả bi xanh và bi...

Đọc tiếp

#Toán lớp 10

1

HQ

Hà Quang Minh

Giáo viên

27 tháng 9 2023

Tổng số khả năng có thể xảy ra của phép thử là \(n\left( \Omega \right) = C_7^2.C_7^2 = 441\)

a) Biến cố “Bốn viên bi lấy ra có cùng màu” xảy ra khi mỗi lần lấy từ 2 hộp đều là hai viên bi xạnh hoặc hai viên bi đỏ. Số kết quả thuận lợi cho biến cố là \(C_4^2.C_5^2 + C_3^2.C_2^2 = 63\)

Vậy xác suất của biến cố “Bốn viên bi lấy ra có cùng màu” là \(P = \frac{{63}}{{441}} = \frac{1}{7}\)

b) Số kết quả thuận lợi cho biến cố “Trong 4 viên bi lấy ra có đúng 1 viên bi xanh” là \(C_4^1.C_3^1.C_2^2 + C_3^2.C_5^1.C_2^1 = 42\)

Vậy xác suất của biến cố “Trong 4 viên bi lấy ra có đúng 1 viên bi xanh” là: \(P = \frac{{42}}{{441}} = \frac{2}{{21}}\)

c) Gọi A là biến cố “Trong 4 viên bi lấy ra có đủ cả bi xanh và bi đỏ”, ta có biến cố đối là \(\overline A \): “4 viên bi lấy ra chỉ có một màu”

\(\overline A \) xảy ra khi 2 lần lấy ra đều được các viên bi cùng màu xanh hoặc cùng màu đỏ

Từ câu a) ta có xác suất của biến cố \(\overline A \) là \(P\left( {\overline A } \right) = \frac{1}{7}\)

Suy ra, xác suất của biến cố A là \(P\left( A \right) = 1 - P\left( {\overline A } \right) = 1 - \frac{1}{7} = \frac{6}{7}\)

Đúng(0)

PT

Pham Trong Bach

31 tháng 5 2018

Hộp bi thứ nhất có 4 viên bi đỏ, 3 viên bi vàng và 5 viên bi xanh. Hộp bi thứ hai có 2 viên bi đỏ, 6 viên bi vàng và 7 viên bi xanh. Chọn ngẫu nhiên mỗi hộp 2 viên bi, tính xác suất sao cho 4 viên bi được chọn luôn có bi đỏ nhưng không có bi xanh. A.181/231 B.181/2310 C.181/2301 D. tất cả...

Đọc tiếp

#Toán lớp 11

1

CM

Cao Minh Tâm

31 tháng 5 2018

Không gian mẫu là chọn ngẫu nhiên mỗi hộp 2 viên bi.

Suy ra số phần tử của không gian mẫu là .

Gọi A là biến cố 4 viên bi được chọn luôn có bi đỏ nhưng không có bi xanh . Ta liệt kê các trường hợp thuận lợi của không gian biến cố A như sau:

● Trường hợp 1. Chọn hộp thứ nhất 2 viên bi đỏ, có cách.

Chọn hộp thứ hai 2 viên bi từ 8 viên bi (2 đỏ và 6 vàng), có cách.

Do đó trường hợp này có cách.

● Trường hợp 2. Chọn hộp thứ nhất 1 viên bi đỏ và 1 viên bi vàng, có cách.

Chọn hộp thứ hai 2 viên bi từ 8 viên bi (2 đỏ và 6 vàng), có cách.

Do đó trường hợp này có cách.

● Trường hợp 3. Chọn hộp thứ nhất 2 viên bi vàng, có cách.

Chọn hộp thứ hai 2 viên bi đỏ hoặc 1 viên bi đỏ và 1 viên bi vàng, có cách.

Do đó trường hợp này có cách.

Suy ra số phần tử của biến cố A là

Vậy xác suất cần tính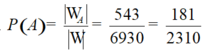

Chọn B.

Đúng(1)

PT

Pham Trong Bach

11 tháng 11 2019

Có hai chiếc hộp. Hộp A đựng 3 bi xanh và 5 bi vàng; Hộp B đựng 2 bi đỏ và 3 bi xanh. Lấy ngẫu nhiên một hộp, rồi lấy một viên bi từ hộp đó. Xác suất để lấy được bị xanh là.

A. 39 40

B. 55 96

C. 34 175

D. 39 80

#Mẫu giáo

1