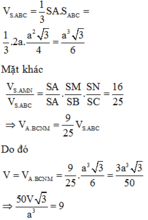Trên hình 85, các tam giác ABC và A'B'C' có cạn chung BC = 3 cm. CA= C'A' = 2cm, góc ABC = A'B'C' = 30 độ nhưng hai tam giác đó không bằng nhawu. Tại sao ở đây không thể áp dụng trường hợp (c.g.c) để kết luận \(\Delta\) ABC =\(\Delta\) A'B'C'
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


ngọc anh , tớ cũng muốn giúp cậu lắm nhưng tớ ko bít làm đành chịu thôi

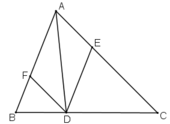
a) Tứ giác AEDF là hình bình hành.
Vì có DE // AF, DF // AE (gt) (theo định nghĩa)
b) Hình bình hành AEDF là hình thoi khi AD là tia phân giác của góc A. Vậy nếu D là giao điểm của tia phân giác góc A với cạnh BC thì AEDF là hình thoi.
c) Nếu ΔABC vuông tại A thì AEDF là hình chữ nhật (vì là hình bình hành có một góc vuông).
d) Nếu ABC vuông tại A và D là giao điểm của tia phân giác của góc A với cạnh BC thì AEDF là hình vuông (vì vừa là hình chữ nhật, vừa là hình thoi).

a) Quan sát hình ta đã thấy diện tích tam giác ADC < diện tích tam giác ABC nhỉ? :)
Nhưng để rõ hơn thì: Có DC = 1/3 BC => DC = 1/2 BD
=> diện tích tam giác ADC = 1/2 diện tích tam giác ABC
b) Vì diện tích tam giác ADC = 1/2 diện tích tam giác ABC
=> DK = 1/2 BH
=> DK = 1/2 x 8,1
=> DK = 4,05 (đơn vị)

Chọn D
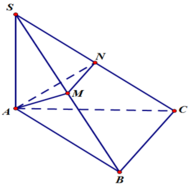
Thể tích khối chóp S. ABC là:
![]()
Do SA=AB=AC=a nên các tam giác SAC, SAB cân tại A.
Theo đề bài M, N là hình chiếu của A trên SB, SC nên M, N lần lượt là trung điểm SB, SC.
Khi đó:
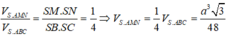
Vậy thể tích khối chóp A. BCNM là:


4cm B C A 3cm 85 M 25 N 30
Trên nữa mặt phẳng bờ chứa tia BA, ABM=25 độ, ABC=85 độ
=>Tia BM nằm giữa 2 tia OA và OC.
=>ABM + MBC = ABC
Thay số: 25 + MBC = 85
MBC = 85 - 25 = 60
Trên nửa mp bờ chứa tia BM, BMN=30 ĐỘ,BMC=60 ĐỘ
=>Tia BN nằm giữa 2 tia BM và BC (1).
=>BMN + BNC = BMC
Thay số: 30 + BNC = 60
BNC = 60 - 30 = 30
=> BMN =BNC = 30 (2)
Từ (1) và (2), kết luận BN là tia phân giác của BMC.
Chúc bạn học tốt!!!