\(\dfrac{x}{5}=\dfrac{y}{3},x^2-y^2=4\)với x,y>0
tìm x,y
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
24 tháng 9 2022
a: \(=\dfrac{3}{2}\sqrt{6}+\dfrac{2}{3}\sqrt{6}-2\sqrt{3}=\dfrac{13}{6}\sqrt{6}-2\sqrt{3}\)
b: \(VT=\dfrac{\sqrt{xy}\left(\sqrt{x}+\sqrt{y}\right)}{\sqrt{xy}}\cdot\left(\sqrt{x}+\sqrt{y}\right)=\left(\sqrt{x}+\sqrt{y}\right)^2\)
c: \(VT=\dfrac{\sqrt{y}}{\sqrt{x}\left(\sqrt{x}-\sqrt{y}\right)}+\dfrac{\sqrt{x}}{\sqrt{y}\left(\sqrt{y}-\sqrt{x}\right)}\)
\(=\dfrac{y-x}{\sqrt{xy}\left(\sqrt{x}-\sqrt{y}\right)}=\dfrac{-\left(\sqrt{x}+\sqrt{y}\right)}{\sqrt{xy}}\)
H9
HT.Phong (9A5)
CTVHS
1 tháng 10 2023
a) \(\dfrac{y}{x}\cdot\sqrt{\dfrac{x^2}{y^4}}\)
\(=\dfrac{y}{x}\cdot\dfrac{\sqrt{x^2}}{\sqrt{\left(y^2\right)^2}}\)
\(=\dfrac{y}{x}\cdot\dfrac{x}{y^2}\)
\(=\dfrac{1}{y}\)
b) \(\dfrac{5}{2}x^3y^3\cdot\sqrt{\dfrac{16}{x^4y^8}}\)
\(=\dfrac{5}{2}x^3y^3\cdot\dfrac{\sqrt{16}}{\sqrt{\left(x^2y^4\right)^2}}\)
\(=\dfrac{5}{2}x^3y^3\cdot\dfrac{4}{x^2y^4}\)
\(=\dfrac{20x^3y^3}{2x^2y^4}\)
\(=\dfrac{10x}{y}\)
c) \(ab^2\sqrt{\dfrac{3}{a^2b^4}}\)
\(=ab^2\dfrac{\sqrt{3}}{\sqrt{\left(ab^2\right)^2}}\)
\(=ab^2\cdot\dfrac{\sqrt{3}}{ab^2}\)
\(=\sqrt{3}\)
T
1 tháng 10 2023
\(a,\dfrac{y}{x}\cdot\sqrt{\dfrac{x^2}{y^4}}\left(y\ge0;x,y\ne0\right)\) (sửa đề)
\(=\dfrac{y}{x}\cdot\dfrac{\sqrt{x^2}}{\sqrt{y^4}}\)
\(=\dfrac{y}{x}\cdot\dfrac{x}{\sqrt{\left(y^2\right)^2}}\)
\(=\dfrac{y}{x}\cdot\dfrac{x}{y^2}\)
\(=\dfrac{1}{y}\)
\(---\)
\(b,\dfrac{5}{2}x^3y^3\cdot\sqrt{\dfrac{16}{x^4y^8}}\left(x,y\ne0\right)\)
\(=\dfrac{5}{2}x^3y^3\cdot\dfrac{\sqrt{16}}{\sqrt{x^4y^8}}\)
\(=\dfrac{5x^3y^3}{2}\cdot\dfrac{4}{x^2y^4}\)
\(=\dfrac{5x\cdot2}{y}\)
\(=\dfrac{10x}{y}\)
\(---\)
\(c,ab^2\sqrt{\dfrac{3}{a^2b^4}}\left(a>0;b\ne0\right)\) (sửa đề)
\(=ab^2\cdot\dfrac{\sqrt{3}}{\sqrt{a^2b^4}}\)
\(=\dfrac{ab^2\sqrt{3}}{\sqrt{\left(ab^2\right)^2}}\)
\(=\dfrac{ab^2\sqrt{3}}{ab^2}\)
\(=\sqrt{3}\)
#\(Toru\)
28 tháng 1 2022
a, \(\dfrac{x}{2}=-\dfrac{5}{y}\Rightarrow xy=-10\Rightarrow x;y\inƯ\left(-10\right)=\left\{\pm1;\pm2;\pm5;\pm10\right\}\)
| x | 1 | -1 | 2 | -2 | 5 | -5 | 10 | -10 |
| y | -10 | 10 | -5 | 5 | -2 | 2 | -1 | 1 |
c, \(\dfrac{3}{x-1}=y+1\Rightarrow\left(y+1\right)\left(x-1\right)=3\Rightarrow x-1;y+1\inƯ\left(3\right)=\left\{\pm1;\pm3\right\}\)
| x - 1 | 1 | -1 | 3 | -3 |
| y + 1 | 3 | -3 | 1 | -1 |
| x | 2 | 0 | 4 | -2 |
| y | 2 | -4 | 0 | -2 |
28 tháng 1 2022
b: =>xy=12
\(\Leftrightarrow\left(x,y\right)\in\left\{\left(12;1\right);\left(6;2\right);\left(4;3\right)\right\}\)
NV
Nguyễn Việt Lâm
Giáo viên
27 tháng 7 2021
Đặt \(\dfrac{x}{y}+\dfrac{y}{x}=t\Rightarrow\left|t\right|\ge2\)
\(\dfrac{x^2}{y^2}+\dfrac{y^2}{x^2}=t^2-2\)
\(\dfrac{x^4}{y^4}+\dfrac{y^4}{x^4}=\left(\dfrac{x^2}{y^2}+\dfrac{y^2}{x^2}\right)^2-2=\left(t^2-2\right)^2-2=t^4-4t^2+2\)
\(\Rightarrow P=f\left(t\right)=t^4-4t^2+2-\left(t^2-2\right)+t\)
\(f\left(t\right)=t^4-5t^2+t+4\)
Xét hàm \(f\left(t\right)=t^4-5t^2+t+4\) trên \((-\infty;-2]\cup[2;+\infty)\)
\(f'\left(t\right)=g\left(t\right)=4t^3-10t+1\)
\(g\left(t\right)\) bậc 3 nên có tối đa 3 nghiệm
\(g\left(-2\right)=-11\) ; \(g\left(0\right)=1\)
\(\Rightarrow g\left(-2\right).g\left(0\right)< 0\Rightarrow g\left(t\right)=0\) có nghiệm \(t_1\in\left(-2;0\right)\)
\(g\left(1\right)=-5< 0\Rightarrow g\left(0\right).g\left(1\right)< 0\Rightarrow g\left(t\right)\) có nghiệm \(t_2\in\left(0;1\right)\)
\(g\left(2\right)=13\Rightarrow g\left(1\right).g\left(2\right)< 0\Rightarrow g\left(t\right)\) có nghiệm \(t_3\in\left(1;2\right)\)
Dấu \(f'\left(t\right)\):
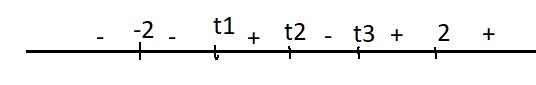
Từ đây ta thấy \(f\left(t\right)\) nghịch biến trên \((-\infty;-2]\) và đồng biến trên \([2;+\infty)\)
Hay GTNN của \(f\left(t\right)\) sẽ rơi vào \(t=-2\) hoặc \(t=2\)
\(f\left(-2\right)=-2\) ; \(f\left(2\right)=2\)
\(\Rightarrow f\left(t\right)_{min}=-2\) khi \(t=-2\) hay \(P_{min}=-2\) khi \(x=-y\)
2 tháng 8 2017
a/\(\dfrac{x}{2}=\dfrac{y}{3}=\dfrac{xy}{2y}=\dfrac{54}{2y}\)
\(\Rightarrow2y\cdot y=54\cdot3\Rightarrow2y^2=162\Rightarrow y^2=\dfrac{162}{2}=81\)
Mà y > 0 (gt) => \(y=\sqrt{81}=9\Rightarrow x=\dfrac{54}{9}=6\)
Vậy..............
b/ \(\dfrac{x}{5}=\dfrac{y}{3}\Rightarrow\dfrac{x^2}{25}=\dfrac{y^2}{9}=\dfrac{x^2-y^2}{25-9}=\dfrac{4}{16}=\dfrac{1}{4}\)
\(\Rightarrow\left\{{}\begin{matrix}x^2=\dfrac{1}{4}\cdot25=\dfrac{25}{4}\\y^2=\dfrac{1}{4}\cdot9=\dfrac{9}{4}\end{matrix}\right.\Rightarrow\left\{{}\begin{matrix}x=\pm\sqrt{\dfrac{25}{4}}=\pm\dfrac{5}{2}\\y=\pm\sqrt{\dfrac{9}{4}}=\pm\dfrac{3}{2}\end{matrix}\right.\)
Vậy.............
c/ x/2 = y/3 => x/10 = y/15
y/5 = z/7 => y/15 = z/21
=> x/10 = y/15 = z/21
Áp dụng t/c của dãy tỉ số = nhau là ra....
7 tháng 10 2022
a: \(=\dfrac{3}{2}\sqrt{6}+\dfrac{2}{3}\sqrt{6}-2\sqrt{6}\)
\(=\dfrac{1}{6}\sqrt{6}\)
b: \(VT=\dfrac{\sqrt{y}}{\sqrt{x}\left(\sqrt{x}-\sqrt{y}\right)}+\dfrac{\sqrt{x}}{\sqrt{y}\left(\sqrt{y}-\sqrt{x}\right)}\)
\(=\dfrac{y-x}{\sqrt{xy}\left(\sqrt{x}-\sqrt{y}\right)}=\dfrac{-\left(\sqrt{x}+\sqrt{y}\right)}{\sqrt{xy}}\)
21 tháng 12 2020
a) Áp dụng tính chất dãy tỉ số bằng nhau ta được:
X/3 = y/4 = x/3 + y/4 = 28/7 = 4
=> x = 4 × 3 = 12
=> y = 4 × 4 = 16
Vậy x = 12, y = 16
B) Áp dụng tính chất dãy tỉ số bằng nhau ta được:
X/2 = y/(-5) = x/2 - y/(-5) = (-7)/7 = -1
=> x = -1 × 2 = -2
=> y = -1 × -5 = 5
Vậy x = -2, y = 5
C) làm tương tự như bài a, b
9 tháng 12 2021
Áp dụng tính chất của dãy tỉ số bằng nhau, ta được:
x8=y12=z15=x+y−z8+12−15=105=2x8=y12=z15=x+y−z8+12−15=105=2
Do đó: x=16; y=24; z=30
\(\dfrac{x}{5}=\dfrac{y}{3}\Leftrightarrow\dfrac{x^2}{25}=\dfrac{y^2}{9}\left(x;y>0\right)\)
Áp dụng ,c dãy tỉ số bằng nhau ta có :
\(\dfrac{x^2}{25}=\dfrac{y^2}{9}=\dfrac{x^2-y^2}{25-9}=\dfrac{4}{16}=\dfrac{1}{4}\)
\(\Leftrightarrow\left\{{}\begin{matrix}\dfrac{x^2}{25}=\dfrac{1}{4}\\\dfrac{y^2}{9}=\dfrac{1}{4}\end{matrix}\right.\) \(\Leftrightarrow\left\{{}\begin{matrix}x=\dfrac{25}{4}\\y=\dfrac{9}{4}\end{matrix}\right.\)
Vậy ..