Question

[Quỳnh Ngân]

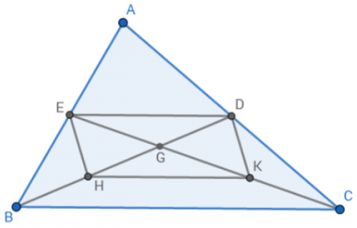
Tam giác ABC, các đưởng trung tuyến BD,CE cắt nhau tại G. Gọi H là trung điểm của GB, Klà trung điểm của GC

a) Tứ giác DEHK là hình j? Vì sao

b) Tam giác ABC có điều kiện j thì tứ giác DEHK là hình chữ nhật?

c) CMR: Nếu BD vuông góc với CE thì tứ giác DEHK là hình thoi

GIÚP MK VỚI MAI MK NỘP R

Answer 1

[Nguyễn Lê Phước Thịnh]

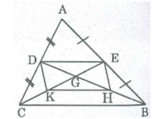
a: Xét ΔABC có

E là trung điểm của AB

D là trung điểm của AC

Do đó: ED là đường trung bình

=>ED//BC và ED=BC/2(1)

Xét ΔGBC có

H là trung điểm của GB

K là trung điểm của GC

Do đó HK là đường trung bình

=>HK//BC và HK=BC/2(2)

Từ (1) và (2) suy ra DE//HK và DE=HK

=>DEHK là hình bình hành

b: Xét ΔAGC có

D là trung điểm của AC

K là trug điểm của GC

Do đó: DK là đường trung bình

=>DK//AG

Để EDKH là hình chữ nhật thì ED\(\perp\)DK

=>AG\(\perp\)BC

Xét ΔBAC có

BD là đường trung tuyến

CE là đường trung tuyến

BD cắt CE tại G

DO đó: G là trọng tâm

=>AG là đường trung tuyến ứng với cạnh BC

Xét ΔBAC có

AG là đường trung tuyến

AG là đường cao

Do đó:ΔBAC cân tại A

c: Hình bình hành EDKH có EK\(\perp\)HD

nên EDKH là hình thoi