Cho tam giác ABC và một điểm O tùy ý . Vẽ tam giác A'B'C' đối xứng với tam giác ABC qua O
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


\(\widehat{BOC}=180^0-\left(\widehat{OBC}+\widehat{OCB}\right)\)
\(=180^0-\left(\widehat{ABC}-\widehat{ABO}+\widehat{ACB}-\widehat{ACO}\right)\)
\(=180^0-\left(180^0-\widehat{BAC}-\widehat{ABO}-\widehat{ACO}\right)\)
\(=\widehat{BAC}+\widehat{ABO}+\widehat{ACO}\)

a) Xét ΔABC vuông tại A và ΔMOC vuông tại M có
\(\widehat{MCO}\) chung
Do đó: ΔABC\(\sim\)ΔMOC(g-g)
b) Xét ΔBMH vuông tại M và ΔBAC vuông tại A có
\(\widehat{MBH}\) chung
Do đó: ΔBMH\(\sim\)ΔBAC(g-g)
Suy ra: \(\dfrac{BM}{BA}=\dfrac{BH}{BC}\)(Các cặp cạnh tương ứng tỉ lệ)
hay \(BM\cdot BC=BA\cdot BH\)(đpcm)

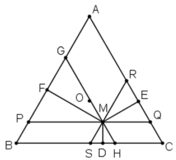
Ta có:
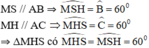
⇒ ΔMHS đều.
MD ⊥ SH nên MD là đường cao đồng thời là trung tuyến của ΔMHS.
⇒ D là trung điểm của HS
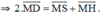
Chứng minh tương tự ta có:
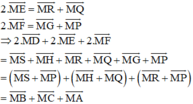
(Vì các tứ giác BSMP, HMQC, MRAG là hình bình hành)
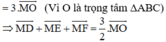

2 M A → + M B → − 3 M C → = 2 ( M C → + C A → ) + ( M C → + C B → ) − 3 M C → = 2 M C → + 2 C A → + M C → + C B → − 3 M C → = 2 C A → + C B → .
Đáp án C


AM=1/3AO
=>OM=2/3AO
BN=1/3BO
=>ON/OB=2/3
CP=1/3CO
=>OP/OC=2/3
Xét ΔOAC có OM/OA=OP/OC
nên MP//AC và MP/AC=OM/MA
=>ΔOMP đồng dạng với ΔOAC
=>S OMP/S OAC=(OM/OA)^2=(2/3)^2=4/9
Xét ΔOAB có OM/OA=ON/OB
nên MN//AB
=>ΔOMN đồng dạng với ΔOAB
=>S OMN/S OAB=(OM/OA)^2=(2/3)^2=4/9
Xét ΔOBC có ON/OB=OP/OC
nên NP//BC
=>ΔONP đồng dạng với ΔOBC
=>S ONP/S OBC=(ON/OB)^2=4/9
=>S MNP=4/9*S ABC=40cm2
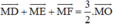
đoạn thẳng:
AA', CC',BB' vẽ đứt khúc nha bạn