Tìm m để hàm số y=x3-6x2+mx+1 đồng biến trên khoảng(0;dương vô cùng)
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
CM
2 tháng 11 2017
Chọn D.
Cách 1: Tập xác định: D = R. Ta có 
+) Trường hợp 1:
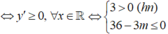
+) Trường hợp 2: Hàm số đồng biến trên (0; +∞) ⇔ y' = 0 có hai nghiệm x1; x2 thỏa mãn x1 < x2 ≤ 0(*)
-) Trường hợp 2.1: y’ = 0 có nghiệm x = 0 suy ra m = 0.
Nghiệm còn lại của y’ = 0 là x = 4 (không thỏa (*))
-) Trường hợp 2.2: y’ = 0 có hai nghiệm x1; x2 thỏa mãn:
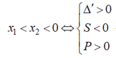
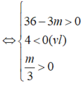
Kết hợp 2 trường hợp, vậy m ≥ 12
CM
16 tháng 3 2017
Chọn C.
. Hàm số đồng biến trên (0;+
∞
)
)
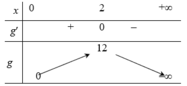
Lập bảng biến thiên của g(x) trên (0;+ ∞ )
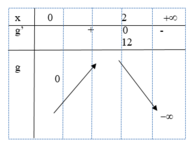
Dựa vào bảng biến thiên, kết luận 
Lập bảng biến thiên của g(x) trên
CM
13 tháng 8 2018
Đáp án A
Ta có y ' = 3 x 2 − 12 x + m
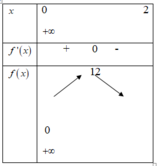
Hàm số đồng biến trên y = f ' x
Ta có f ' x = − 6 x + 12 ⇒ f ' x = 0 ⇔ x = 2 . Ta có bảng biến thiên hàm số f(x) như trên
Từ bảng biến thiên, suy ra f x 0 ; + ∞ ≤ 12 ⇒ m ≥ f x 0 ; + ∞ ⇔ m ≥ 12
CM
6 tháng 11 2017
Đáp án D
Cách giải:
+ 
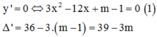
=> Hàm số đồng biến trên 
+ 
Phương trình (1) có 2 nghiệm phân biệt 
Theo đinh lí Viet ta có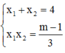 
Khi đó, để hàm số đồng biến trên khoảng (1;+∞) thì
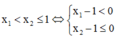
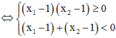
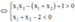
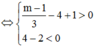( vô lí )
Vậy m ≥ 13
Mà 
Số giá trị của m thỏa mãn là: 2018 - 13 + 1 = 2006
NV
Nguyễn Việt Lâm
Giáo viên
14 tháng 1 2021
\(y'=3x^2+m+\dfrac{1}{x^6}\ge0\) ; \(\forall x>0\)
\(\Leftrightarrow3x^2+\dfrac{1}{x^6}\ge-m\)
\(\Leftrightarrow-m\le\min\limits_{x>0}\left(3x^2+\dfrac{1}{x^6}\right)\)
Ta có: \(3x^2+\dfrac{1}{x^6}=x^2+x^2+x^2+\dfrac{1}{x^6}\ge4\sqrt[4]{\dfrac{x^6}{x^6}}=4\)
\(\Rightarrow-m\le4\Rightarrow m\ge-4\)
Lời giải:
Ta có: \(y=x^3-6x^2+mx+1\Rightarrow y'=3x^2-12x+m\)
Để hàm $y$ luôn đồng biến với mọi \(x\in (0;+\infty)\Rightarrow y'=3x^2-12x+m\geq 0\forall x\in (0;+\infty)\)
\(\Leftrightarrow m\geq 12x-3x^2\forall x\in (0;+\infty)\)
\(\Leftrightarrow m\geq \max (12x-3x^2)\forall x\in (0;+\infty)\)
Ta thấy \(12x-3x^2=-3(x-2)^2+12\leq 12\)
Dấu bằng xảy ra khi \(x=2\in (0;+\infty)\Rightarrow \max(12x-3x^2)\forall x\in (0;+\infty)\) là $12$
Vậy \(m\geq 12\)