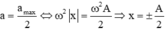Câu 1:Li độ của một vật phụ thuộc vào thời gian theo phương trình :x=12\(\sin\left(\omega t\right)\)-\(16\sin^3\left(\omega t\right)\).Vật dao động điều hòa thì gia tốc có độ lớn cực đại là? Câu 2:Độ...

Ta có: \(x\left( t \right) = {x_1}\left( t \right) + {x_2}\left( t \right) = 2\left[ {\cos \left( {\frac{\pi }{3}t + \frac{\pi }{6}} \right) + \cos \left( {\frac{\pi }{3}t - \frac{\pi }{3}} \right)} \right]\)

\(2\left[ {\cos \left( {\frac{{\frac{\pi }{3}t + \frac{\pi }{6} + \frac{\pi }{3}t - \frac{\pi }{3}}}{2}} \right).\cos \left( {\frac{{\frac{\pi }{3}t + \frac{\pi }{6} - \frac{\pi }{3}t + \frac{\pi }{3}}}{2}} \right)} \right] = 2\left[2. {\cos \left( {\frac{\pi }{3}t - \frac{\pi }{{12}}} \right).\cos \frac{\pi }{4}} \right] = 2\sqrt 2 \cos \left( {\frac{\pi }{3}t - \frac{\pi }{{12}}} \right)\)

Vậy biên độ là \(2\sqrt 2 \), pha ban đầu \( - \frac{\pi }{{12}}\)

Đúng(0)

QT

Quoc Tran Anh Le

Giáo viên

21 tháng 9 2023

Trong vật lí, ta biết rằng phương trình tổng quát của một vật dao động điều hòa cho bởi công thức \(x\left( t \right) = A\cos (\omega t + \varphi )\), trong đó t là thời điểm (tính bằng giây), x(t) là li độ của vật tại thời điểm t, A là biên độ dao động (A > 0), \(\omega t + \varphi \) là pha dao động tại thời điểm t và \(\varphi \in \left[ { - \pi ;\pi } \right]\) là pha ban đầu của dao động. Dao động điều hòa này...

Đọc tiếp

#Toán lớp 11

1

HQ

Hà Quang Minh

Giáo viên

21 tháng 9 2023

a) Biên độ dao động \(A = - 5\); Pha ban đầu của dao động: \(\varphi = 0\)

b) Pha dao động tại thời điểm \(t = 2\) à \(\omega t + \varphi = 4\pi .2 = 8\pi \)

Chu kỳ \(T = \frac{{2\pi }}{\omega } = \frac{{2\pi }}{{4\pi }} = 0,2\)

Trong khoảng thời gian 2 giây, số dao động toàn phần vật thực hiện được là: \(\frac{2}{{0,2}} = 10\) (dao động)

Đúng(0)

QT

Quoc Tran Anh Le

Giáo viên

21 tháng 9 2023

Một dao động điều hòa có phương trình li độ dao động là: \(x = A\cos \left( {\omega t + \varphi } \right)\), trong đó t là thời gian tính bằng giây, A là biên độ dao động và x là li độ dao động đều được tính bằng centimet. Khi đó, chu kì T của dao động là \(T = \frac{{2\pi }}{\omega }\). Xác định giá trị của li độ khi \(t = 0,t = \frac{T}{4},t = \frac{T}{2},t = \frac{{3T}}{4},t = T\) và vẽ đồ thị biểu diễn li độ của dao...

Đọc tiếp

#Toán lớp 11

1

HQ

Hà Quang Minh

Giáo viên

21 tháng 9 2023

Ta có

\(\begin{array}{l}t = 0 \Rightarrow \omega t = 0\\t = \frac{T}{4} \Rightarrow \omega t = \omega .\frac{{\frac{{2\pi }}{\omega }}}{4} = \frac{\pi }{2}\\t = \frac{T}{2} \Rightarrow \omega t = \omega .\frac{{\frac{{2\pi }}{\omega }}}{2} = \pi \\t = \frac{{3T}}{4} \Rightarrow \omega t = \omega .\frac{{3.\frac{{2\pi }}{\omega }}}{4} = \frac{{3\pi }}{2}\\t = T \Rightarrow \omega t = \omega .\frac{{2\pi }}{\omega } = 2\pi \end{array}\)

a) \(A = 3cm,\varphi = 0\)

+) Với t=0 thì \(x = 3\cos \left( {\omega .0 + 0} \right) = 3\)

+) Với \(t = \frac{T}{4}\)thì \(x = 3\cos \left( {\frac{\pi }{2} + 0} \right) = 0\)

+) Với \(t = \frac{T}{2}\)thì \(x = 3\cos \left( {\pi + 0} \right) = - 3\)

+)Với \(t = \frac{{3T}}{4}\)thì \(x = 3\cos \left( {\frac{{3\pi }}{2} + 0} \right) = 0\)

+Với \(t = T\)thì \(x = 3\cos \left( {2\pi + 0} \right) = 3\)

b) \(A = 3cm,\varphi = - \frac{\pi }{2}\)

+) Với t=0 thì \(x = 3\cos \left( {0 - \frac{\pi }{2}} \right) = 0\)

+) Với \(t = \frac{T}{4}\)thì \(x = 3\cos \left( {\frac{\pi }{2} - \frac{\pi }{2}} \right) = 3\)

+) Với \(t = \frac{T}{2}\)thì \(x = 3\cos \left( {\pi - \frac{\pi }{2}} \right) = 0\)

+)Với \(t = \frac{{3T}}{4}\)thì \(x = 3\cos \left( {\frac{{3\pi }}{2} - \frac{\pi }{2}} \right) = 3\)

+Với \(t = T\)thì \(x = 3\cos \left( {2\pi - \frac{\pi }{2}} \right) = 0\)

c) \(A = 3cm,\varphi = \frac{\pi }{2}\)

+) Với t=0 thì \(x = 3\cos \left( {0 + \frac{\pi }{2}} \right) = 0\)

+) Với \(t = \frac{T}{4}\)thì \(x = 3\cos \left( {\frac{\pi }{2} + \frac{\pi }{2}} \right) = 3\)

+) Với \(t = \frac{T}{2}\)thì \(x = 3\cos \left( {\pi + \frac{\pi }{2}} \right) = 0\)

+)Với \(t = \frac{{3T}}{4}\)thì \(x = 3\cos \left( {\frac{{3\pi }}{2} + \frac{\pi }{2}} \right) = 3\)

+Với \(t = T\)thì \(x = 3\cos \left( {2\pi + \frac{\pi }{2}} \right) = 0\)

Đúng(0)

HD

Hoàng Đức Long

6 tháng 12 2018

Một vật nhỏ dao động điều hòa theo phương trình x = Acos4pt (t tính bằng s). Tính từ t=0, khoảng thời gian ngắn nhất để gia tốc của vật có độ lớn bằng một nửa độ lớn gia tốc cực đại là

A. 0,083s.

B. 0,167s.

C. 0,104s.

D. 0,125s.

#Mẫu giáo

1

VT

Vũ Thành Nam

6 tháng 12 2018

Đáp án A

Chu kì dao động của vật = 0,5s.

Gia tốc có độ lớn bằng một nửa độ lớn gia tốc cực đại:

Ta thấy rằng, tính từ t =0, khoảng thời gian ngắn nhất để gia tốc của vật có độ lớn bằng một nửa độ lớn gia tốc cực đại là t = T/6 = 0,083s

Đúng(0)

HD

Hoàng Đức Long

6 tháng 3 2019

Một vật nhỏ dao động điều hòa theo phương trình x = Acos4πt (t tính bằng s). Tính từ t = 0 khoảng thời gian ngắn nhất để gia tốc của vật có độ lớn bằng một nửa độ lớn gia tốc cực đại là

A. 0,083 s.

B. 0,104 s.

C. 0,167 s.

D. 0,125 s.

#Mẫu giáo

1

VT

Vũ Thành Nam

6 tháng 3 2019

Đáp án A

Đúng(0)

LA

Lê Anh Thư

19 tháng 10 2023

Một vật dao động điều hòa với tần số góc \(\omega\) = 5rad/s . Khi t = 0 , vật đi qua vị trí có li độ x = -2cm và có vận tốc 10cm/s hướng về vị trí biên gần nhấta) Viết phương trình dao động của vậtb) Tính tốc độ cực đại và gia tốc cực đạic) Tính quãng đường vật đi được sau 1,4\(\pi\) s...

Đọc tiếp

#Vật lý lớp 11

1

TC

Trên con đường thành công không có....

19 tháng 10 2023

Giả sử pt dao động của vật có dạng:

\(x=Acos\left(5t+\varphi\right)\left(cm\right)\)

\(\Rightarrow v=-5Asin\left(5t+\varphi\right)=5Acos\left(\dfrac{\pi}{2}+5t+\varphi\right)\left(\text{cm/s}\right)\)

Tại \(t=0:\)\(\left\{{}\begin{matrix}x=-2\left(cm\right)\\v=10\left(\text{cm/s}\right)\end{matrix}\right.\)

\(\Rightarrow\left\{{}\begin{matrix}x_0=Acos\varphi=-2\left(cm\right)\\v_0=5Acos\left(\dfrac{\pi}{2}+\varphi\right)=10\left(\text{cm/s}\right)\end{matrix}\right.\)

\(\Leftrightarrow\left\{{}\begin{matrix}cos\varphi=-\dfrac{2}{A}\left(1\right)\\5A\left(cos\dfrac{\pi}{2}.cos\varphi-sin\dfrac{\pi}{2}.sin\varphi\right)=10\end{matrix}\right.\)

\(\Rightarrow5A.\left(-sin\varphi\right)=10\Leftrightarrow sin\varphi=\dfrac{-2}{A}\left(2\right)\)

Từ \(\left(1\right);\left(2\right)\Rightarrow\varphi=\dfrac{-3\pi}{4}\left(rad\right);A=2\sqrt{2}\left(cm\right)\)

Vậy ta có ptdđ của vật: \(x=2\sqrt{2}cos\left(5t-\dfrac{3\pi}{4}\right)\left(cm\right)\)

b)\(v_{max}=\omega A=5A=10\sqrt{2}\left(\text{cm/s}\right)\)

\(a_{max}=\omega^2A=50\sqrt{2}\left(\text{cm/s}^2\right)\)

c) \(\alpha=\Delta t.\omega=1,4\pi.5=7\pi\left(rad\right)=6\pi+\pi\left(rad\right)\)

\(\Rightarrow S=3.4A+2\sqrt{2}-2+2\sqrt{2}+2=12A+4\sqrt{2}=28\sqrt{2}\left(cm\right)\)

Đúng(2)

HD

Hoàng Đức Long

23 tháng 11 2019

Hình vẽ trên là đồ thị biểu diễn sự phụ thuộc của li độ x vào thời gian t của một vật dao động điều hòa. Tốc độ cực đại của vật bằng: A. 5,24 cm/s. B. 1,05 cm/s. C. 10,47 cm/s. D. 6,28...