 giải giúp mình bài này với ạ mình cảm ơn
giải giúp mình bài này với ạ mình cảm ơn
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


3:
1: Gọi tuổi mẹ và tuổi con hiện nay lần lượt là x,y
Theo đề, ta có: x=2,3y và x-16=7,5(y-16)
=>x-2,3y=0 và x-7,5y=-120+16=-104
=>x=46 và y=20
Gọi số năm nữa để tuổi mẹ gấp đôi tuổi con là a
Theo đề, ta có
a+46=2a+40
=>-a=-6
=>a=6
2:
Xe đi 210m trong 30-16=14s
=>V=210/14=15m/s
Chiều dài là:
15*16=240(m)

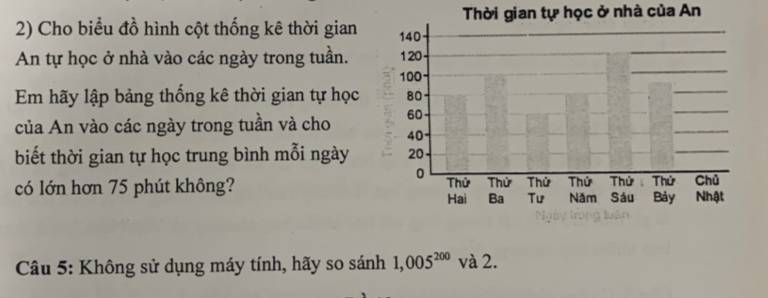
bài 1
| thứ | 2 | 3 | 4 | 5 | 6 | 7 | CN |
| TG học | 80p | 100p | 60p | 80p | 120p | 90p | 0p |
TBC TG bạn học 1 ngày là : (80*2+100+60+120+90+0)/7 \(\approx\) 76
Vậy TG bạn học 1 ngày là hơn 75p
2
ko bt nhưng chắc chắn là 1,005200
LỚN HƠN NHA

3:
1: Gọi chiều dài, chiều rộng lần lượt là a,b
Theo đề, ta có: 6/5a*4/5b=ab-30
=>ab=750
=>S=750
2:
Sau 1,5h thì xe 1 đi được 15*1,5=22,5(km)
Hiệu vận tốc là 20-15=5(km/h)
Thời gian hai xe đuổi kịp nhau là:
22,5/5=4,5(h)
=>Người 1 đi đến B sau 5h
ĐỘ dài AB là:
15*5=75km


`sin3x sinx+sin(x-π/3) cos (x-π/6)=0`
`<=> 1/2 (cos2x - cos4x) + 1/2(-sin π/6 + sin (2x-π/2)=0`
`<=> cos2x-cos4x-1/2+ sin(2x-π/2)=0`
`<=>cos2x-cos4x-1/2+ sin2x .cos π/2 - cos2x. sinπ/2=0`
`<=> cos2x - cos4x - cos2x = 1/2`
`<=> cos4x = cos(2π)/3`
`<=>` \(\left[{}\begin{matrix}4x=\dfrac{2\text{π}}{3}+k2\text{π}\\4x=\dfrac{-2\text{π}}{3}+k2\text{π}\end{matrix}\right.\)
`<=>` \(\left[{}\begin{matrix}x=\dfrac{\text{π}}{6}+k\dfrac{\text{π}}{2}\\x=-\dfrac{\text{π}}{6}+k\dfrac{\text{π}}{2}\end{matrix}\right.\)

\(x=\sqrt[3]{9+4\sqrt{5}}+\sqrt[3]{9-4\sqrt{5}}\)
\(\Rightarrow x^3=9+4\sqrt{5}+9-4\sqrt{5}+3\sqrt[3]{\left(9+4\sqrt[]{5}\right)\left(9-4\sqrt{5}\right)}\left(\sqrt[3]{9+4\sqrt{5}}+\sqrt[3]{9-4\sqrt{5}}\right)\)
\(=18+3\sqrt{81-80}.x=18+3x\)\(\Rightarrow x^3-3x=18\left(1\right)\)
\(y=\sqrt[3]{3+2\sqrt{2}}+\sqrt[3]{3-2\sqrt{2}}\)
\(\Rightarrow y^3=3+2\sqrt{2}+3-2\sqrt{2}+3\sqrt[3]{\left(3+2\sqrt{2}\right)\left(3-2\sqrt{2}\right)}\left(\sqrt[3]{3+2\sqrt{2}}+\sqrt[3]{3-2\sqrt{2}}\right)\)
\(=6+3\sqrt[3]{9-8}.y=6+3y\)\(\Rightarrow y^3-3y=6\left(2\right)\)
\(\left(1\right),\left(2\right)\Rightarrow P=x^3+y^3-3\left(x+y\right)+1996=x^3-3x+y^3-3y+1996\)
\(=18+6+1996=2020\)

bạn tự vẽ hình giúp mik nha
a. xét \(\Delta ADN\) và \(\Delta BAM\) có
AB=AD(gt)
\(\widehat{ADN}=\widehat{BAM}=90^o\)
DN=MA(N,M là trung điểm của cạnh DC,AD)
\(\Rightarrow\Delta ADN\sim\Delta BAM\left(c.g.c\right)\)
\(\Rightarrow\widehat{DNA}=\widehat{AMB}\)
mà:\(\widehat{DNA}+\widehat{DAN}=90^o\Rightarrow\widehat{BMA}+\widehat{DAN}=90^o\)
\(\Rightarrow\Delta MAI\) vuông tại I
\(\Rightarrow AI\perp MI\) hay \(MB\perp AN\)
b.ta có M là trung điểm của AD\(\Rightarrow AM=\dfrac{1}{2}AD=\sqrt{5}\)
trong \(\Delta MAB\) vuông tại A có
\(MB=\sqrt{AM^2+AB^2}=\sqrt{\sqrt{5^2}+\left(2\sqrt{5}\right)^2}=5\)
\(AM^2=MB.MI\Rightarrow MI=\dfrac{AM^2}{MB}=\dfrac{\sqrt{5^2}}{5^5}=0,2\)
\(AI.MB=AM.AB\Rightarrow AI=\dfrac{AM.AB}{MB}=\dfrac{\sqrt{5}.2\sqrt{5}}{5}\)=2
c.IB=MB-MI=5-0,2=4,8
\(S_{\Delta AIB}=\dfrac{AI.IB}{2}=\)\(\dfrac{2.4,8}{2}=4,8\)
\(S_{\Delta ADN}=\dfrac{AD.DN}{2}=\dfrac{2\sqrt{5}.\sqrt{5}}{2}=5\)
\(S_{\Delta ABCD}=\left(2\sqrt{5}\right)^2=20\)
\(S_{BINC}=S_{ABCD}-S_{\Delta AIB}-S_{\Delta DAN}\)=20-4,8-5=10,2


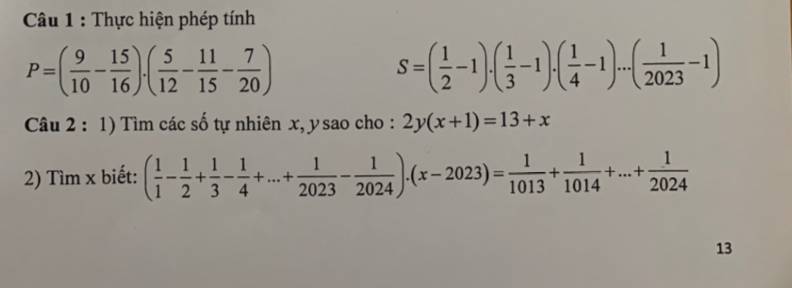
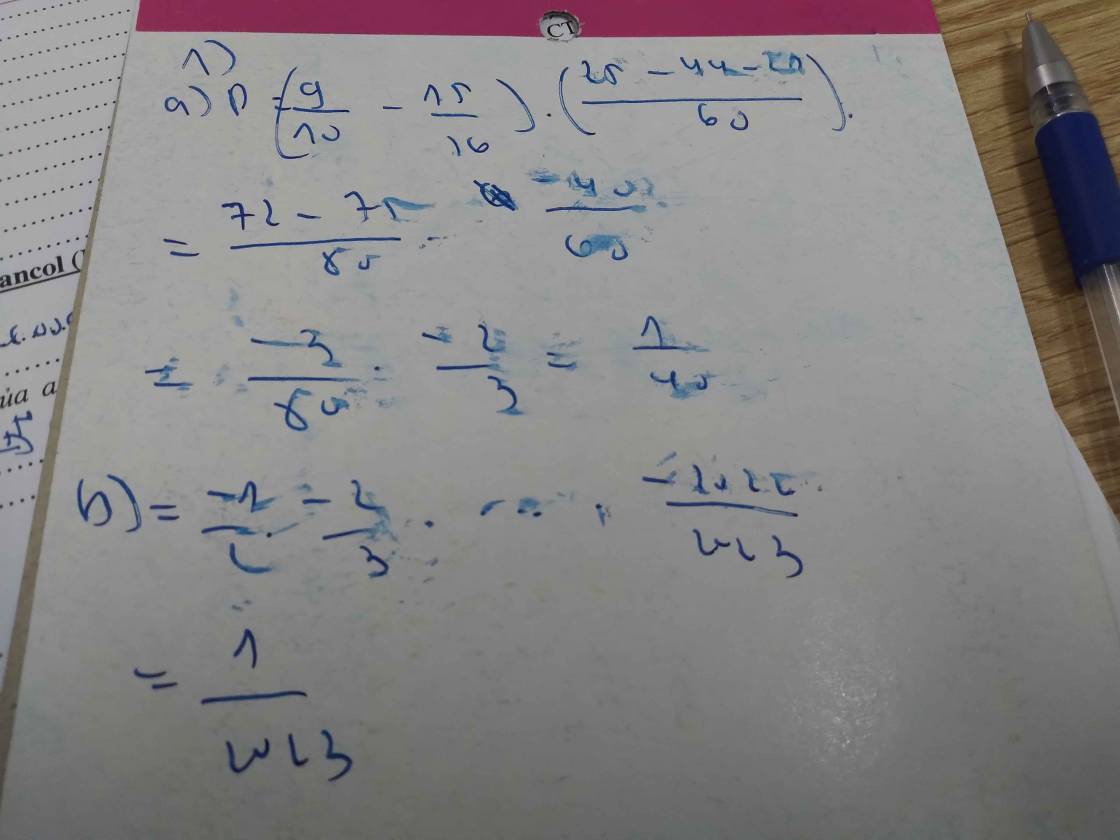

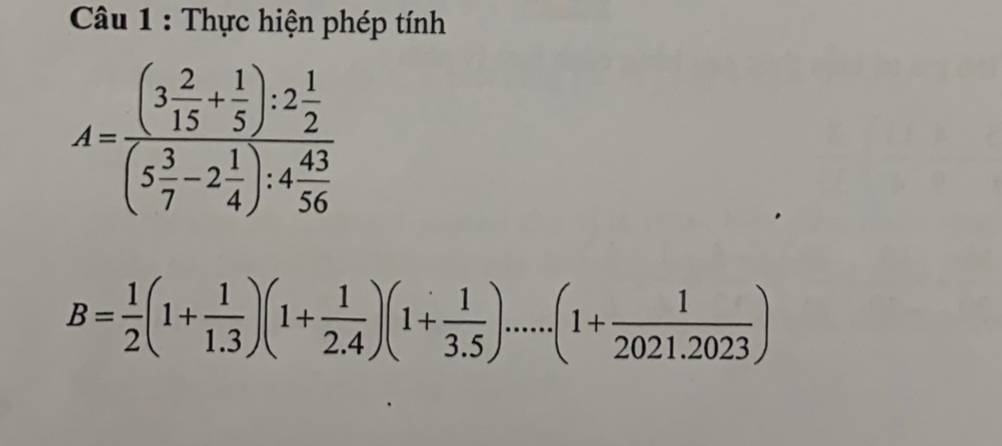


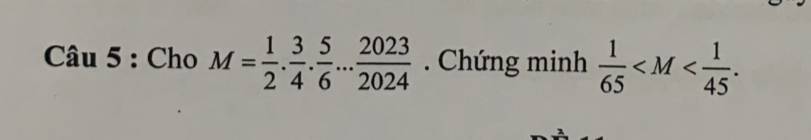

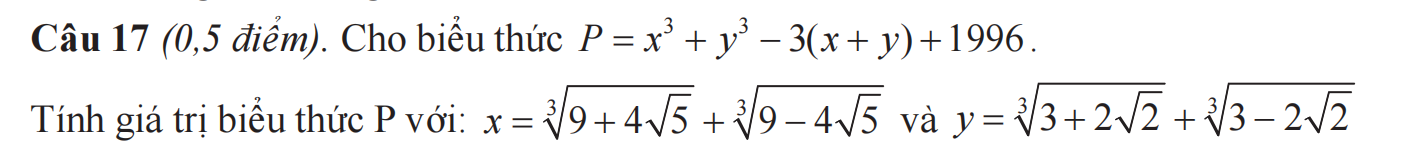 cảm ơn
cảm ơn 


\(A=\frac{3}{\sqrt{x}+1}-\frac{1}{\sqrt{x}-1}-\frac{\sqrt{x}-3}{x-1}\)
\(=\frac{3\left(\sqrt{x}-1\right)}{\left(\sqrt{x}-1\right)\left(\sqrt{x}+1\right)}-\frac{\sqrt{x}+1}{\left(\sqrt{x}-1\right)\left(\sqrt{x}+1\right)}-\frac{\sqrt{x}-3}{\left(\sqrt{x}-1\right)\left(\sqrt{x}+1\right)}\)
\(=\frac{3\sqrt{x}-3-\sqrt{x}+1-\sqrt{x}+3}{\left(\sqrt{x}-1\right)\left(\sqrt{x}+1\right)}=\frac{\sqrt{x}+1}{\left(\sqrt{x}-1\right)\left(\sqrt{x}+1\right)}=\frac{1}{\sqrt{x}-1}\)
\(B=\left(1-\frac{\sqrt{2}}{x-\sqrt{2}}+\frac{\sqrt{2}}{x+\sqrt{2}}\right)\div\frac{x-\sqrt{6}}{x^2-2}\)
\(=\left[\frac{x^2-2}{\left(x-\sqrt{2}\right)\left(x+\sqrt{2}\right)}-\frac{\sqrt{2}\left(x+\sqrt{2}\right)}{\left(x-\sqrt{2}\right)\left(x+\sqrt{2}\right)}+\frac{\sqrt{2}\left(x-\sqrt{2}\right)}{\left(x-\sqrt{2}\right)\left(x+\sqrt{2}\right)}\right]\cdot\frac{\left(x-\sqrt{2}\right)\left(x+\sqrt{2}\right)}{x-\sqrt{6}}\)
\(=\frac{x^2-2-\sqrt{2}x-2+\sqrt{2}x-2}{\left(x-\sqrt{2}\right)\left(x+\sqrt{2}\right)}\cdot\frac{\left(x-\sqrt{2}\right)\left(x+\sqrt{2}\right)}{x-\sqrt{6}}\)
\(=\frac{x^2-6}{x-\sqrt{6}}=\frac{\left(x-\sqrt{6}\right)\left(x+\sqrt{6}\right)}{x-\sqrt{6}}=x+\sqrt{6}\)