
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


\(x=\sqrt[3]{9+4\sqrt{5}}+\sqrt[3]{9-4\sqrt{5}}\)
\(\Rightarrow x^3=9+4\sqrt{5}+9-4\sqrt{5}+3\sqrt[3]{\left(9+4\sqrt[]{5}\right)\left(9-4\sqrt{5}\right)}\left(\sqrt[3]{9+4\sqrt{5}}+\sqrt[3]{9-4\sqrt{5}}\right)\)
\(=18+3\sqrt{81-80}.x=18+3x\)\(\Rightarrow x^3-3x=18\left(1\right)\)
\(y=\sqrt[3]{3+2\sqrt{2}}+\sqrt[3]{3-2\sqrt{2}}\)
\(\Rightarrow y^3=3+2\sqrt{2}+3-2\sqrt{2}+3\sqrt[3]{\left(3+2\sqrt{2}\right)\left(3-2\sqrt{2}\right)}\left(\sqrt[3]{3+2\sqrt{2}}+\sqrt[3]{3-2\sqrt{2}}\right)\)
\(=6+3\sqrt[3]{9-8}.y=6+3y\)\(\Rightarrow y^3-3y=6\left(2\right)\)
\(\left(1\right),\left(2\right)\Rightarrow P=x^3+y^3-3\left(x+y\right)+1996=x^3-3x+y^3-3y+1996\)
\(=18+6+1996=2020\)

bạn tự vẽ hình giúp mik nha
a. xét \(\Delta ADN\) và \(\Delta BAM\) có
AB=AD(gt)
\(\widehat{ADN}=\widehat{BAM}=90^o\)
DN=MA(N,M là trung điểm của cạnh DC,AD)
\(\Rightarrow\Delta ADN\sim\Delta BAM\left(c.g.c\right)\)
\(\Rightarrow\widehat{DNA}=\widehat{AMB}\)
mà:\(\widehat{DNA}+\widehat{DAN}=90^o\Rightarrow\widehat{BMA}+\widehat{DAN}=90^o\)
\(\Rightarrow\Delta MAI\) vuông tại I
\(\Rightarrow AI\perp MI\) hay \(MB\perp AN\)
b.ta có M là trung điểm của AD\(\Rightarrow AM=\dfrac{1}{2}AD=\sqrt{5}\)
trong \(\Delta MAB\) vuông tại A có
\(MB=\sqrt{AM^2+AB^2}=\sqrt{\sqrt{5^2}+\left(2\sqrt{5}\right)^2}=5\)
\(AM^2=MB.MI\Rightarrow MI=\dfrac{AM^2}{MB}=\dfrac{\sqrt{5^2}}{5^5}=0,2\)
\(AI.MB=AM.AB\Rightarrow AI=\dfrac{AM.AB}{MB}=\dfrac{\sqrt{5}.2\sqrt{5}}{5}\)=2
c.IB=MB-MI=5-0,2=4,8
\(S_{\Delta AIB}=\dfrac{AI.IB}{2}=\)\(\dfrac{2.4,8}{2}=4,8\)
\(S_{\Delta ADN}=\dfrac{AD.DN}{2}=\dfrac{2\sqrt{5}.\sqrt{5}}{2}=5\)
\(S_{\Delta ABCD}=\left(2\sqrt{5}\right)^2=20\)
\(S_{BINC}=S_{ABCD}-S_{\Delta AIB}-S_{\Delta DAN}\)=20-4,8-5=10,2

a) \(=\sqrt{\left(\sqrt{5}+\sqrt{3}\right)^2}=\sqrt{5}+\sqrt{3}\)
b) \(=\sqrt{\left(\sqrt{2}+1\right)^2}=\sqrt{2}+1\)
c) \(=\sqrt{\left(2\sqrt{2}+3\right)^2}=2\sqrt{2}+3\)
d) \(=\sqrt{\left(3-\sqrt{5}\right)^2}=3-\sqrt{5}\)
e) \(=\sqrt{\left(4-\sqrt{6}\right)^2}=4-\sqrt{6}\)
f) \(=\sqrt{\left(3+\sqrt{7}\right)^2}=3+\sqrt{7}\)
l) \(=\sqrt{\left(\sqrt{2}-\dfrac{1}{2}\right)^2}=\sqrt{2}-\dfrac{1}{2}\)
m) \(=\sqrt{\left(2\sqrt{2}+\dfrac{1}{4}\right)^2}=2\sqrt{2}+\dfrac{1}{4}\)

a: Ta có: BC⊥BA tại B
nên BC là tiếp tuyến của (A;AB)
b: Xét (A) có
CB là tiếp tuyến
CD là tiếp tuyến
Do đó: CB=CD
hay C nằm trên đường trung trực của BD(1)
Ta có: AB=AD
nên A nằm trên đường trung trực của BD(2)
Từ (1) và (2) suy ra AC là đường trung trực của BD
hay AC\(\perp\)BD
Giúp mình luôn câu c d được không:((( sắp hết h rồi mà không bt làm

2:
1+cot^2a=1/sin^2a
=>1/sin^2a=1681/81
=>sin^2a=81/1681
=>sin a=9/41
=>cosa=40/41
tan a=1:40/9=9/40


\(1,ĐK:x\ge2\\ PT\Leftrightarrow\sqrt{3x-6}+x-2-\left(\sqrt{2x-3}-1\right)=0\\ \Leftrightarrow\dfrac{3\left(x-2\right)}{\sqrt{3x-6}}+\left(x-2\right)-\dfrac{2\left(x-2\right)}{\sqrt{2x-3}+1}=0\\ \Leftrightarrow\left(x-2\right)\left(\dfrac{3}{\sqrt{3x-6}}-\dfrac{2}{\sqrt{2x-3}+1}+1\right)=0\\ \Leftrightarrow\left[{}\begin{matrix}x=2\left(tm\right)\\\dfrac{3}{\sqrt{3x-6}}-\dfrac{2}{\sqrt{2x-3}+1}+1=0\left(1\right)\end{matrix}\right.\)
Với \(x>2\Leftrightarrow-\dfrac{2}{\sqrt{2x-3}+1}>-\dfrac{2}{1+1}=-1\left(3x-6\ne0\right)\)
\(\Leftrightarrow\left(1\right)>0-1+1=0\left(vn\right)\)
Vậy \(x=2\)
\(2,ĐK:x\ge-1\)
Đặt \(\left\{{}\begin{matrix}\sqrt{x+1}=a\\\sqrt{x^2-x+1}=b\end{matrix}\right.\left(a,b\ge0\right)\Leftrightarrow a^2+b^2=x^2+2\)
\(PT\Leftrightarrow2a^2+2b^2-5ab=0\\ \Leftrightarrow\left(a-2b\right)\left(2a-b\right)=0\\ \Leftrightarrow\left[{}\begin{matrix}a=2b\\b=2a\end{matrix}\right.\)
Với \(a=2b\Leftrightarrow x+1=4x^2-4x+4\left(vn\right)\)
Với \(b=2a\Leftrightarrow4x+4=x^2-x+1\Leftrightarrow x^2-5x-3=0\Leftrightarrow\left[{}\begin{matrix}x=\dfrac{5+\sqrt{37}}{2}\left(tm\right)\\x=\dfrac{5-\sqrt{37}}{2}\left(tm\right)\end{matrix}\right.\)
Vậy ...

Bài 2 :
a, Ta có đồ thị :
b, Ta có : \(\tan a=3\)
\(\Rightarrow a\approx71,5^o\)

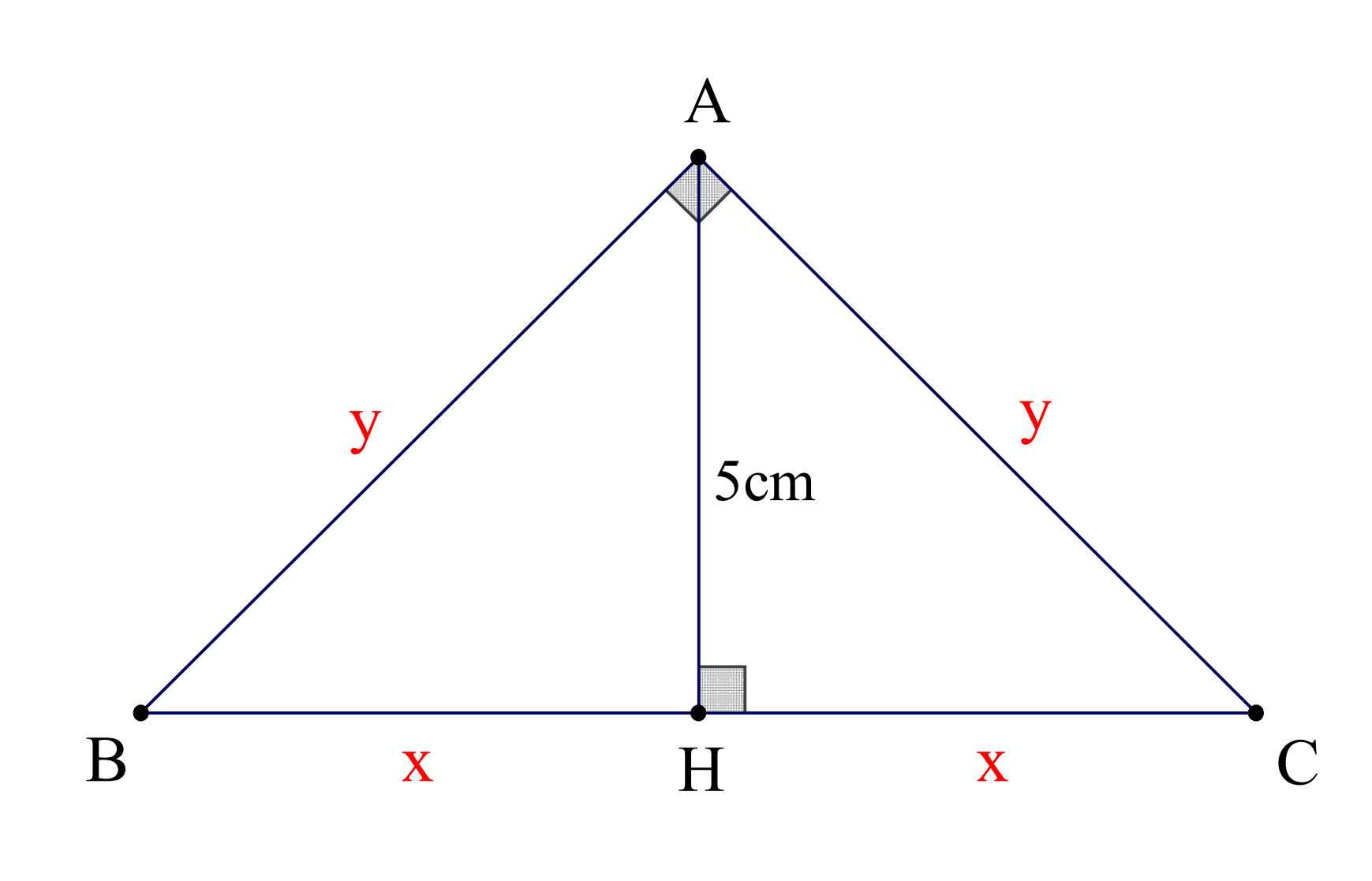
Áp dụng HTL trong tam giác ABC vuông tại A có đường cao AH:
\(AH^2=BH.HC\)
\(\Rightarrow x^2=5^2\Rightarrow x=5\left(cm\right)\)
\(AB^2=BH.BC\)
\(\Rightarrow AB=\sqrt{BH.BC}=\sqrt{5.\left(5+5\right)}\)
\(\Rightarrow y=5\sqrt{2}\left(cm\right)\)
 giải giúp mình bài này với ạ mình cảm ơn
giải giúp mình bài này với ạ mình cảm ơn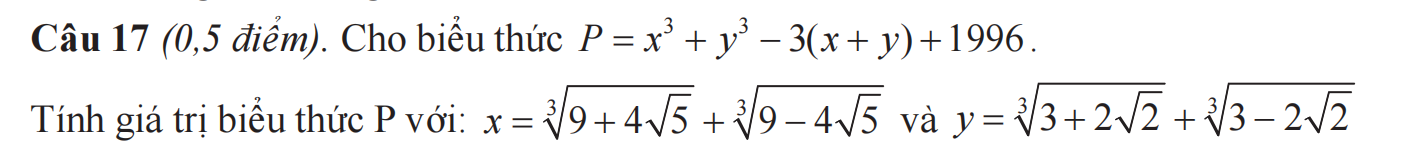 cảm ơn
cảm ơn 


 Giúp mình bài này với ạ, mình cần lời giải chi tiết. Mình cảm ơn
Giúp mình bài này với ạ, mình cần lời giải chi tiết. Mình cảm ơn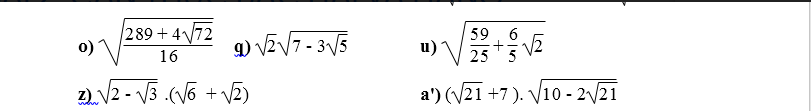





\(A=\frac{3}{\sqrt{x}+1}-\frac{1}{\sqrt{x}-1}-\frac{\sqrt{x}-3}{x-1}\)
\(=\frac{3\left(\sqrt{x}-1\right)}{\left(\sqrt{x}-1\right)\left(\sqrt{x}+1\right)}-\frac{\sqrt{x}+1}{\left(\sqrt{x}-1\right)\left(\sqrt{x}+1\right)}-\frac{\sqrt{x}-3}{\left(\sqrt{x}-1\right)\left(\sqrt{x}+1\right)}\)
\(=\frac{3\sqrt{x}-3-\sqrt{x}+1-\sqrt{x}+3}{\left(\sqrt{x}-1\right)\left(\sqrt{x}+1\right)}=\frac{\sqrt{x}+1}{\left(\sqrt{x}-1\right)\left(\sqrt{x}+1\right)}=\frac{1}{\sqrt{x}-1}\)
\(B=\left(1-\frac{\sqrt{2}}{x-\sqrt{2}}+\frac{\sqrt{2}}{x+\sqrt{2}}\right)\div\frac{x-\sqrt{6}}{x^2-2}\)
\(=\left[\frac{x^2-2}{\left(x-\sqrt{2}\right)\left(x+\sqrt{2}\right)}-\frac{\sqrt{2}\left(x+\sqrt{2}\right)}{\left(x-\sqrt{2}\right)\left(x+\sqrt{2}\right)}+\frac{\sqrt{2}\left(x-\sqrt{2}\right)}{\left(x-\sqrt{2}\right)\left(x+\sqrt{2}\right)}\right]\cdot\frac{\left(x-\sqrt{2}\right)\left(x+\sqrt{2}\right)}{x-\sqrt{6}}\)
\(=\frac{x^2-2-\sqrt{2}x-2+\sqrt{2}x-2}{\left(x-\sqrt{2}\right)\left(x+\sqrt{2}\right)}\cdot\frac{\left(x-\sqrt{2}\right)\left(x+\sqrt{2}\right)}{x-\sqrt{6}}\)
\(=\frac{x^2-6}{x-\sqrt{6}}=\frac{\left(x-\sqrt{6}\right)\left(x+\sqrt{6}\right)}{x-\sqrt{6}}=x+\sqrt{6}\)