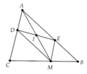
1. Cho \(\Delta\) ABC cân tại A, M là một điểm trên cạnh BC ( M không là trung điểm cạnh BC ). Qua M kẻ đường thẳng song song với AB cắt cạnh AC tại D, đường thẳng song song với AC cắt AB tại E.
a) Chứng minh \(\Delta\) MCD cân.
b) Chứng minh AE = CD
c) Lấy điểm F đối xứng với điểm M qua đường thẳng DE. Tứ giác ADEF là hình gì ?
d) Gọi K là giao điểm của DF và AB. Chứng minh chu vi \(\Delta\) AKD không phụ thuộc vị trí điểm M trên cạnh BC.
Mọi người giúp em với. Cảm ơn mọi người nhiều lắm ạ. ![]()

bạn tự vẽ hình nhé, mình chỉ giải được a,b thôi
a. tam giác ABC cân=> góc B= góc C
mà DM//AB => góc DMC= góc B(đồng vị)
=> góc DMC= góc C =>tam giác DMC cân
b. ME//AC
MD//AB
=> ADME là hình bình hành=> AE= DM
mà DM=DC (tam giác DMC cân)=> AE= DC
Cảm ơn bạn