1.Cho các số dương x và y tm: $\dfrac{x^2 1}{y^2}=1$ Tìm Min A=$\dfrac{x}{y} \dfrac{y}{x}$ 2. Cho a,b,c>0 . CM: \(\dfrac{a}{a \sqrt{\left(a b\right)\left(a c\right)}} \dfrac{b}{b \sqrt{\left(b c...

LD

Linh Đan Hoàng

14 tháng 10 2017

1.Cho các số dương x và y tm: $\dfrac{x^2+1}{y^2}=1$ Tìm Min A=$\dfrac{x}{y}+\dfrac{y}{x}$ 2. Cho a,b,c>0 . CM: $\dfrac{a}{a+\sqrt{\left(a+b\right)\left(a+c\right)}}+\dfrac{b}{b+\sqrt{\left(b+c\right)\left(b+a\right)}}+\dfrac{c}{c+\sqrt{\left(a+c\right)\left(c+b\right)}}\le1$ Giúp mk vs mình đag cần gấp lắm vì ko có chủ đề là Bđt nên mk ms đặt là căn bậc 2 nhak ...

Đọc tiếp

#Toán lớp 9

1

UK

Unruly Kid

15 tháng 10 2017

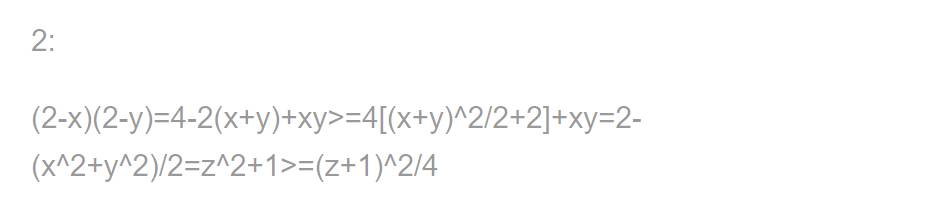
Dễ chứng minh được:

$\sqrt{\left(a+b\right)\left(a+c\right)}\ge\sqrt{ac}+\sqrt{ab}$

Do đó, ta có:

$\sum\limits_{cyc}=\dfrac{a}{a+\sqrt{\left(a+b\right)\left(a+c\right)}}\le\sum_{cyc}\dfrac{a}{a+\sqrt{ac}+\sqrt{ab}}=\dfrac{\sqrt{a}}{\sqrt{a}+\sqrt{b}+\sqrt{c}}=1$

Vậy: BĐT đã được chứng minh. Đẳng thức xảy ra khi và chỉ khi a=b=c

Đúng(0)

PD

Phạm Duy Phát

26 tháng 2 2021

1.a,b,c là các số thực dương. CM $\left(\dfrac{\sqrt{ab}}{\sqrt{a+b}}+\dfrac{\sqrt{bc}}{\sqrt{b+c}}\right)\left(\dfrac{1}{\sqrt{a+b}}+\dfrac{1}{\sqrt{b+c}}\right)\le2$2. x,y là các số nguyên sao cho $x^2-2xy-y^2$ ;$xy-2y^2-x$ đều chia hết cho 5Chứng minh $2x^2+y^2+2x+y$ cũng chia hết cho 53. cho $a_1a_2...a_{50}$ là các số nguyên thoả mãn $1\le a_1\le a_2...\le a_{50}\le50;a_1+a_2+...+a_{50}=100$ chứng minh rằng từ các số đã cho có thể chọn đc một...

Đọc tiếp

#Toán lớp 9

0

HM

Hi Mn

12 tháng 4 2023

1. a,b,c>0 và a+b+c=2017$CM:\Sigma\dfrac{2017a-a^2}{bc}\ge\sqrt{2}\left(\Sigma\sqrt{\dfrac{2017-a}{a}}\right)$2. cho x,y,z tm: $x^2+y^2+z^2=3$$CM:8\left(2-x\right)\left(2-y\right)\left(2-z\right)\ge\left(x+yz\right)\left(y+zx\right)\left(z+xy\right)$3. a,b,c>0...

Đọc tiếp

#Toán lớp 10

1

NL

Nguyễn Lê Phước Thịnh

13 tháng 4 2023

loading...

Tương tự, ta được:

$\left(2-y\right)\left(2-z\right)>=\dfrac{\left(x+1\right)^2}{4}$

và $\left(2-z\right)\left(2-x\right)>=\left(\dfrac{y+1}{2}\right)^2$

=>8(2-x)(2-y)(2-z)>=(x+1)(y+1)(z+1)

(x+yz)(y+zx)<=(x+y+yz+xz)^2/4=(x+y)^2*(z+1)^2/4<=(x^2+y^2)(z+1)^2/4

Tương tự, ta cũng co:

$\left(y+xz\right)\left(z+y\right)< =\dfrac{\left(y^2+z^2\right)\left(x+1\right)^2}{2}$

và $\left(z+xy\right)\left(x+yz\right)< =\dfrac{\left(z^2+x^2\right)\left(y+1\right)^2}{2}$

Do đó, ta được:

$\left(x+yz\right)\left(y+zx\right)\left(z+xy\right)< =\left(x+1\right)\left(y+1\right)\left(z+1\right)$

=>ĐPCM

Đúng(0)

PN

Phạm NI NA

16 tháng 6 2017

a:$\dfrac{b}{\left(a-4\right)^2}.\sqrt{\dfrac{\left(a-4\right)^4}{b^2}}\left(b0;a\ne4\right)$ b:$\dfrac{x\sqrt{x}-y\sqrt{y}}{\sqrt{x}-\sqrt{y}}\left(x\ge0;y\ge0;x\ne0\right)$ c:$\dfrac{a}{\left(b-2\right)^2}.\sqrt{\dfrac{\left(b-2\right)^4}{a^2}\left(a0;b\ne2\right)}$ d:$\dfrac{x}{\left(y-3\right)^2}.\sqrt{\dfrac{\left(y-3\right)^2}{x^2}\left(x0;y\ne3\right)}$ e:2x...

Đọc tiếp

#Toán lớp 9

2

NH

Nguyễn Huy Tú

16 tháng 6 2017

a, $\dfrac{b}{\left(a-4\right)^2}.\sqrt{\dfrac{\left(a-4\right)^4}{b^2}}=\dfrac{b}{\left(a-4\right)^2}.\dfrac{\left(a-4\right)^2}{b}=1$

b, Đặt $B=\dfrac{x\sqrt{x}-y\sqrt{y}}{\sqrt{x}-\sqrt{y}}$

$\sqrt{x}=a,\sqrt{y}=b$

Ta có: $B=\dfrac{a^3-b^3}{a-b}=\dfrac{\left(a-b\right)\left(a^2+ab+b^2\right)}{a-b}=a^2+ab+b^2$

$\Rightarrow B=x+\sqrt{xy}+y$

Vậy...

c, $\dfrac{a}{\left(b-2\right)^2}.\sqrt{\dfrac{\left(b-2\right)^4}{a^2}}=\dfrac{a}{\left(b-2\right)^2}.\dfrac{\left(b-2\right)^2}{a}=1$

d, $2x+\dfrac{\sqrt{1-6x+9x^2}}{3x-1}=2x+\dfrac{\sqrt{\left(3x-1\right)^2}}{3x-1}=2x+1$

Đúng(0)

TD

Thảo Đinh Thị Phương

16 tháng 6 2017

a: $b(a-4)2.\sqrt(a-4)4b2(b>0;a\neq4)b(a-4)2.(a-4)4b2(b>0;a\neq4)$

$= $\dfrac{b}{\left(a-4\right)}.\dfrac{\sqrt{\left[\left(a-4\right)^2\right]^2}}{\sqrt{b^2}}$$

=$\dfrac{b}{\left(a-4\right)^2}.\dfrac{\left(a-4\right)^2}{b}$

= 1 ( nhân tử với tử mẫu với mẫu rồi rút gọn)

b: $x\sqrtx-y\sqrty\sqrtx-\sqrty(x\geq0;y\geq0;x\neq0)xx-yyx-y(x\geq0;y\geq0;x\neq0)$

$=$\dfrac{\sqrt{x^3}-\sqrt{y^3}}{\sqrt{x}-\sqrt{y}}$$

=$\dfrac{\left(\sqrt{x}\right)^3-\left(\sqrt{y}\right)^3}{\sqrt{x}-\sqrt{y}}$

=$\dfrac{\left(\sqrt{x}-\sqrt{y}\right).\left(x+\sqrt{xy}+y\right)}{\sqrt{x}-\sqrt{y}}$(áp dụng hằng đẳng thức )

= (x+$\sqrt{xy}$+y)

c: $a(b-2)2.\sqrt(b-2)4a2(a>0;b\neq2)a(b-2)2.(b-2)4a2(a>0;b\neq2)$

$Tương tự câu a$

d: $x(y-3)2.\sqrt(y-3)2x2(x>0;y\neq3)x(y-3)2.(y-3)2x2(x>0;y\neq3)$

$tương tự câu a$

e:2x + $\sqrt1-6x+9x23x-1$

$= $2x+\dfrac{\sqrt{\left(3x\right)^2-6x+1}}{3x-1}$$

= 2x+$\dfrac{\sqrt{\left(3x-1\right)^2}}{3x-1}$(hằng đẳng thức)

=2x+$\dfrac{3x-1}{3x-1}$

=2x+1

Đúng(0)

HM

Hi Mn

8 tháng 1 2023

+) Tìm min

$E=\dfrac{1+\sqrt[3]{x}+\sqrt[3]{y}+\sqrt[3]{z}}{xy+yz+zx}$

+) Tìm max và min

$F=\dfrac{a-b}{c}+\dfrac{b-c}{a}+\dfrac{c-a}{b}$

Trong đó a,b,c>0 và $min\left\{a,b,c\right\}\ge\dfrac{1}{4}max\left\{a,b,c\right\}$

#Toán lớp 10

0

MH

Minh Hiếu

14 tháng 4 2023

+) Giải hệ pt: $\left\{{}\begin{matrix}4\sqrt{x^2+4y-5}=y^2-x+10\\x^3+\left(1-y\right)x^2=\left(x+4\right)y\end{matrix}\right.$

+) Cho a,b,c>0 và a+b+c=2017

CM: $\dfrac{2017a-a^2}{bc}+\dfrac{2017b-b^2}{ca}+\dfrac{2017c-c^2}{ab}\ge\sqrt{2}\left(\Sigma\sqrt{\dfrac{2017-a}{a}}\right)$

#Toán lớp 10

2

TT

Trần Tuấn Hoàng

15 tháng 4 2023

+) Bài bất đẳng thức:

$\dfrac{2017a-a^2}{bc}=\dfrac{\left(a+b+c\right)a-a^2}{bc}=\dfrac{ab+ca}{bc}=\dfrac{a}{c}+\dfrac{a}{b}\left(1\right)$

Tương tự: $\left\{{}\begin{matrix}\dfrac{2017b-b^2}{ca}=\dfrac{b}{a}+\dfrac{b}{c}\left(2\right)\\\dfrac{2017c-c^2}{ab}=\dfrac{c}{a}+\dfrac{c}{b}\left(3\right)\end{matrix}\right.$

$\left(1\right)+\left(2\right)+\left(3\right)\Rightarrow\dfrac{2017a-a^2}{bc}+\dfrac{2017b-b^2}{bc}+\dfrac{2017c-c^2}{ab}=\dfrac{a+b}{c}+\dfrac{b+c}{a}+\dfrac{c+a}{b}$

$\sqrt{2}\left(\sum\sqrt{\dfrac{2017-a}{a}}\right)=\sqrt{2}\left(\sum\sqrt{\dfrac{\left(a+b+c\right)-a}{a}}\right)=\sqrt{2}\left(\sqrt{\dfrac{b+c}{a}}+\sqrt{\dfrac{c+a}{b}}+\sqrt{\dfrac{a+b}{2}}\right)$

Bất đẳng thức cần chứng minh tương đương với:

$\dfrac{a+b}{c}+\dfrac{b+c}{a}+\dfrac{c+a}{b}\ge\sqrt{2}\left(\sqrt{\dfrac{a+b}{c}}+\sqrt{\dfrac{b+c}{a}}+\sqrt{\dfrac{c+a}{b}}\right)$

*Có: $\sqrt{2.\dfrac{a+b}{c}}+\sqrt{2.\dfrac{b+c}{a}}+\sqrt{2.\dfrac{c+a}{b}}\le\dfrac{2+\dfrac{a+b}{c}}{2}+\dfrac{2+\dfrac{b+c}{a}}{2}+\dfrac{2+\dfrac{c+a}{b}}{2}=3+\dfrac{\dfrac{a+b}{c}+\dfrac{b+c}{a}+\dfrac{c+a}{b}}{2}$

Ta chỉ cần chứng minh:

$\dfrac{a+b}{c}+\dfrac{b+c}{a}+\dfrac{c+a}{b}\ge3+\dfrac{\dfrac{a+b}{c}+\dfrac{b+c}{a}+\dfrac{c+a}{b}}{2}$

hay $\dfrac{a+b}{c}+\dfrac{b+c}{a}+\dfrac{c+a}{b}\ge6$ (cái này chị tự chứng minh nhé)

Đúng(11)

HT

Hàng Tô Kiều Trang

15 tháng 4 2023

b giỏi quá

Đúng(1)

MT

Mai Tiến Đỗ

23 tháng 1 2021

1) cho các số thực dương a,b thỏa mãn $3a+b\le1$. Tìm Min của $P=\dfrac{1}{a}+\dfrac{1}{\sqrt{ab}}$2) Với hai số thực a,b không âm thỏa mãn $a^2+b^2=4$. Tìm Max $M=\dfrac{ab}{a+b+2}$3) Cho x,y khác 0 thỏa mãn $\left(x+y\right)xy=x^2+y^2-xy$. Tìm...

Đọc tiếp

#Toán lớp 9

2

TM

Trần Minh Hoàng

23 tháng 1 2021

1) Áp dụng bất đẳng thức AM - GM và bất đẳng thức Schwarz:

$P=\dfrac{1}{a}+\dfrac{1}{\sqrt{ab}}\ge\dfrac{1}{a}+\dfrac{1}{\dfrac{a+b}{2}}\ge\dfrac{4}{a+\dfrac{a+b}{2}}=\dfrac{8}{3a+b}\ge8$.

Đẳng thức xảy ra khi a = b = $\dfrac{1}{4}$.

Đúng(1)

NV

Nguyễn Việt Lâm

Giáo viên

23 tháng 1 2021

2.

$4=a^2+b^2\ge\dfrac{1}{2}\left(a+b\right)^2\Rightarrow a+b\le2\sqrt{2}$

Đồng thời $\left(a+b\right)^2\ge a^2+b^2\Rightarrow a+b\ge2$

$M\le\dfrac{\left(a+b\right)^2}{4\left(a+b+2\right)}=\dfrac{x^2}{4\left(x+2\right)}$ (với $x=a+b\Rightarrow2\le x\le2\sqrt{2}$ )

$M\le\dfrac{x^2}{4\left(x+2\right)}-\sqrt{2}+1+\sqrt{2}-1$

$M\le\dfrac{\left(2\sqrt{2}-x\right)\left(x+4-2\sqrt{2}\right)}{4\left(x+2\right)}+\sqrt{2}-1\le\sqrt{2}-1$

Dấu "=" xảy ra khi $x=2\sqrt{2}$ hay $a=b=\sqrt{2}$

3. Chia 2 vế giả thiết cho $x^2y^2$

$\dfrac{1}{x}+\dfrac{1}{y}=\dfrac{1}{x^2}+\dfrac{1}{y^2}-\dfrac{1}{xy}\ge\dfrac{1}{4}\left(\dfrac{1}{x}+\dfrac{1}{y}\right)^2$

$\Rightarrow0\le\dfrac{1}{x}+\dfrac{1}{y}\le4$

$A=\left(\dfrac{1}{x}+\dfrac{1}{y}\right)\left(\dfrac{1}{x^2}+\dfrac{1}{y^2}-\dfrac{1}{xy}\right)=\left(\dfrac{1}{x}+\dfrac{1}{y}\right)^2\le16$

Dấu "=" xảy ra khi $x=y=\dfrac{1}{2}$

Đúng(1)

QB

Quyên Bùi

11 tháng 1 2018

Câu 1: Cho bt: A= $\left(\dfrac{1}{\sqrt{1+x}}+\sqrt{1-x}\right):\left(\dfrac{1}{\sqrt{1-x^2}}+1\right)$ a) Tìm x để A có nghĩa b) Rút gọn c) Tính A với x =$\dfrac{\sqrt{3}}{2+\sqrt{3}}$ Câu 2: Cho bt B= $\left(\dfrac{x-y}{\sqrt{x}-\sqrt{y}}+\dfrac{x\sqrt{x}-y\sqrt{y}}{y-x}\right):\left(\dfrac{\left(\sqrt{x}-\sqrt{y}\right)^2+\sqrt{xy}}{\sqrt{x}+\sqrt{y}}\right)$ a) Rút gọn b) CM B$\ge$0 c) So sánh B với...

Đọc tiếp

#Toán lớp 9

1

PT

Phạm Thị Hoa

12 tháng 1 2018

Hỏi đáp Toán

Đúng(0)

MH

Minh Hiếu

24 tháng 1 2022

1. Phân tích đa thức thành nhân tử:$x^5-x^4+\left(y+2\right)x^3+\left(y-2\right)x^2+yx+y^2$2. Cho các số dương thỏa mãn:$\dfrac{b+c}{a^2}+\dfrac{c+a}{b^2}+\dfrac{a+b}{c^2}=2\left(\dfrac{1}{a}+\dfrac{1}{b}+\dfrac{1}{c}\right)$Tính giá trị biểu thức sau: $P=\left(a-b\right)^{2009}+\left(b-c\right)^{2009}+\left(c-a\right)^{2009}$3. Cho x,y,x đôi một khác nhau và khác 0. Chứng minh rằng nếu:$\dfrac{x^2-yz}{a}=\dfrac{y^2-xz}{b}=\dfrac{z^2-xy}{c}$ thì ta...

Đọc tiếp

#Toán lớp 9

3

S

Sun ...

24 tháng 1 2022

k làm đc k cần phải ghi zậy mô ha

Đúng(0)

NV

Nguyễn Việt Lâm

Giáo viên

24 tháng 1 2022

1.

$y^2+y\left(x^3+x^2+x\right)+x^5-x^4+2x^3-2x^2$

$\Delta=\left(x^3+x^2+x\right)^2-4\left(x^5-x^4+2x^3-2x^2\right)$

$=\left(x^3-x^2+3x\right)^2$

$\Rightarrow\left[{}\begin{matrix}y=\dfrac{-x^3-x^2-x+x^3-x^2+3x}{2}=-x^2+x\\y=\dfrac{-x^3-x^2-x-x^3+x^2-3x}{2}=-x^3-2x\end{matrix}\right.$

Hay đa thức trên có thể phân tích thành:

$\left(x^2-x+y\right)\left(x^3+2x+y\right)$

Dựa vào đó em tự tách cho phù hợp

Đúng(1)

DT

Đào Thu Hiền

23 tháng 7 2023

Bài 1: Cho a, b, c > 1. CMR: $a^{\log_bc}+b^{\log_ca}+c^{\log_ab}\ge3\sqrt[3]{abc}$

Bài 2: Cho các số x, y, z > 0 thoả mãn: $\dfrac{x\left(y+z-x\right)}{logx}=\dfrac{y\left(z+x-y\right)}{logy}=\dfrac{z\left(x+y-z\right)}{logz}$. CMR: x^y.y^x = y^z.z^y = x^z.z^x

#Toán lớp 12

0

Chúng tôi đề xuất

Tài nguyên

Ứng dụng mobile

Bảng xếp hạng

Các khóa học có thể bạn quan tâm

Yêu cầu VIP