Cho hàm số:y=a phần x
a) Xác định a để đồ thị hàm số qua điểm A(-3;-2)
b)Tìm tất cả các điểm trên đồ thị hàm số tìm đc ở câu a có các tọa độ đều là số nguyên
Mong mọi người giúp đỡ ^-^
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a: Thay x=-1 và y=1 vào (d), ta được:
-(2m+1)=1
=>2m+1=-1
=>2m=-2
=>m=-1
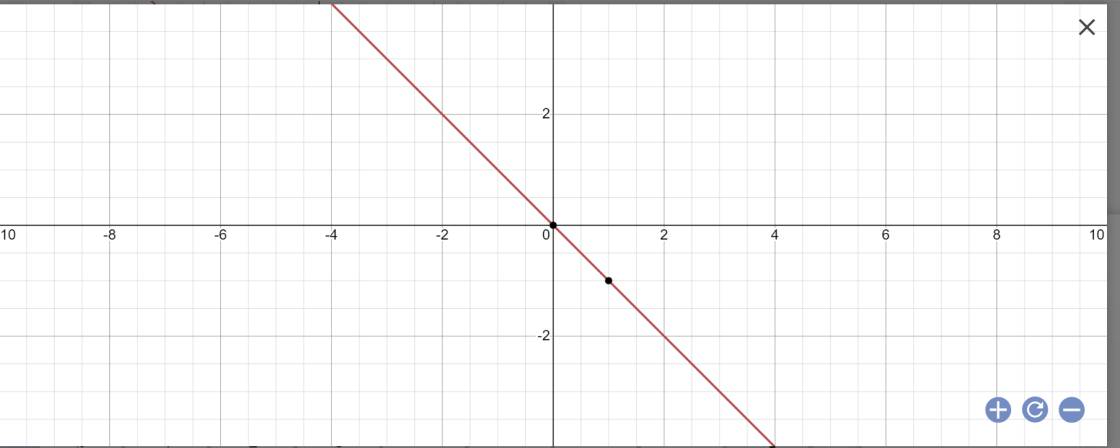
b: y=(-2+1)x=-x

a) Đths \(y=\left(2m+1\right)x\) đi qua \(A\left(-1;1\right)\)
Ta có:
\(y=\left(2m+1\right)x\)
\(\Rightarrow\left(2m+1\right)\left(-1\right)=1\)
\(\Rightarrow2m+1=-1\)
\(\Rightarrow2m=-2\)
\(\Rightarrow m=-1\)
b) Thay \(m=-1\)
\(\Rightarrow y=\left(-2+1\right)x\)
\(\Rightarrow y=-x\)
Lập bảng giá trị:
| \(x\) | \(0\) | \(-2\) |
| \(y=-x\) | \(0\) | \(2\) |
> y > x O -2 2

a: Thay x=-1 và y=1 vào (d), ta được:
-(a-1)+a=1
=>-a+1+a=1
=>1=1(luôn đúng)
b: Thay x=0 và y=3 vào (d), ta được;
0(a-1)+a=3
=>a=3
=>y=2x+3
c: Thay x=-2 và y=0 vào (d), ta được;
-2(a-1)+a=0
=>-2a+2+a=0
=>2-a=0
=>a=2

Xác định hệ số a, biết rằng đồ thị của hàm số y=ax đi qua điểm A(6;2).Điểm B(-9;3), điểm C(7;-2) có thuộc đồ thị hàm số không ? Tìm trên đồ thị của hàm số điểm D có hoành độ bằng -4,điểm E có tung độ bằng 2

a, gọi điểm hàm số (1) luôn đi qua là A(xo,yo) thì xo,yo thỏa mãn (1)
\(=>yo=\left(a-1\right)xo+a< ->a.\left(xo+1\right)-\left(xo+yo\right)=0\)
\(=>\left\{{}\begin{matrix}xo+1=0\\xo+yo=0\end{matrix}\right.\)=>xo=-1,yo=1 vậy.....
b,\(=>x=0,y=3=>\left(1\right):a=3\)(tm)
c,\(=>x=-2,y=0=>\left(1\right):0=\left(a-1\right)\left(-2\right)+a=>a=2\left(tm\right)\)
\(=>y=x+2\) cho x=0=>y=2=>A(0;2)
cho y=0=>x=-2=>B(-2;0)
gọi OH là khoảng cách từ gốc tọa độ đến đồ thị hàm số(1)
\(=>\dfrac{1}{OH^2}=\dfrac{1}{OA^2}+\dfrac{1}{OB^2}=>\dfrac{1}{OH^2}=\dfrac{1}{2^2}+\dfrac{1}{\left(-2\right)^2}=>OH=....\)

\(a,\Leftrightarrow1+m=-2\Leftrightarrow m=-3\\ \Leftrightarrow y=x-3\\ \text{Thay }x=2;y=5\Leftrightarrow5=2-3=-1\left(\text{vô lí}\right)\\ \Leftrightarrow E\notinđths\\ b,\text{PT giao Ox và Oy: }\left\{{}\begin{matrix}y=0\Rightarrow x=-m\Rightarrow E\left(-m;0\right)\Rightarrow OE=\left|m\right|\\x=0\Rightarrow y=m\Rightarrow F\left(0;m\right)\Rightarrow OF=\left|m\right|\end{matrix}\right.\)
Gọi H là chân đường cao từ O đến EF
Áp dụng HTL: \(\dfrac{1}{OH^2}=\dfrac{1}{OE^2}+\dfrac{1}{OF^2}=\dfrac{1}{2m^2}=\dfrac{1}{3^2}=\dfrac{1}{9}\)
\(\Leftrightarrow m^2=\dfrac{9}{2}\Leftrightarrow\left[{}\begin{matrix}m=\dfrac{3}{\sqrt{2}}\\m=-\dfrac{3}{\sqrt{2}}\end{matrix}\right.\)