K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
TK
25 tháng 9 2017
Gọi O la giao điểm hai đường chéo hình bình hành
Từ O kẻ OO' vông góc với d tại O'
Ta có O' là trg điểm của A'O (do cùng vuông góc và song song với D' trên duog thẳng d )
suy ra OO'là dg trg bình cua tam giac AAC
suy ra AA' = 2 OO'(1)
Ta có DD' song song BB' ( do cùng vuông óc với d)
suy ra DD' ,BB' là hình thang
Ta có
OO' song song DD' song song BB' (cùng vuông góc d)(a)
Và O là trug điểm DB(b(
Từ (a) và(b) suy ra O là trung điểm D'B'
suy ra OO là dg2 trung bình của bình thang DD' BB'
suy ra OO' là dg trug bình của hình thang DD' BB'
suy ra D'B' =2OO' (2)
Từ (1) và (2) suy ra AA' =BB' +DD'
nhớ cho mình nha
CM
3 tháng 9 2017
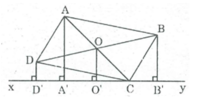
Gọi O là giao điểm của hai đường chéo AC và BD.
Kẻ OO' ⊥ xy
Ta có: BB' ⊥ xy (gt)
DD' ⊥ xy (gt)
Suy ra: BB // OO' // DD'
Tứ giác BB'D'D là hình thang .
OB = OD (t/chất hình bình hành)
Nên O'B' = O'D'
Do đó OO' là đường trung bình của hình thang BB'D'D
⇒ OO' = (BB' + DD') / 2 (tính chất đường trung hình hình thang) (1)
AA' ⊥ xy (gt)
OO' ⊥ xy (theo cách vẽ)
Suy ra: AA' // OO'
Trong ∆ ACA' tacó: OA = OC (tính chất hình bình hành)
OO' // AA' nên OO' là đường trung bình của ∆ ACA'
⇒ OO' = 1/2 AA' (tính chất đường trung bình của tam giác)
⇒ AA' = 2OO' (2)
Tử (1) và (2) suy ra: AA' = BB' + DD'
17 tháng 3 2020
a) Xét ΔOAHΔOAH và ΔOBHΔOBH ta có:
OA = OB (theo giả thiết)
HA = HB (H là trung điểm AB)
OH chung
⇒ΔOAH=ΔOBH(c−c−c)⇒ΔOAH=ΔOBH(c−c−c)
b) Ta có: ΔOAH=ΔOBHΔOAH=ΔOBH (chứng minh trên)
⇒∠AOH=∠BOH⇒∠AOH=∠BOH ( 2 góc tương ứng bằng nhau)
Hay ∠AOC=∠BOC∠AOC=∠BOC
Xét ΔOACΔOAC và ΔOBCΔOBC ta có:
OA = OB (theo giả thiết)
OC chung
∠AOC=∠BOC∠AOC=∠BOC
⇒ΔOAC=ΔOBC(c−g−c)⇒ΔOAC=ΔOBC(c−g−c)
⇒∠OAC=∠OBC⇒∠OAC=∠OBC(2 góc tương ứng)
Mà ∠OAC∠OAC= 900 nên ∠OBC∠OBC = 900
⇒CB⊥OB⇒CB⊥OB( điều phải chứng minh)
c) Ta có: ∠AOC=∠BOC∠AOC=∠BOC (chứng minh trên) (1)
Xét 2 tam giác vuông MIO và MIH ta có:
MI chung
IO = IH (Vì I là trung điểm của OH)
⇒ΔMIO=ΔMIH⇒ΔMIO=ΔMIH (Cạnh góc vuông – cạnh góc vuông)
⇒∠MOI=∠MHI⇒∠MOI=∠MHI (2 góc tương ứng)
Hay∠AOC=∠MHIHay∠AOC=∠MHI (2)
Từ (1) và (2) ta có: ∠BOC=∠MHI∠BOC=∠MHI (cặp góc ở vị trí so le trong)
⇒MH//OB⇒MH//OB (*)
Lại có:
HK⊥BCOB⊥BC}⇒HK//OBHK⊥BCOB⊥BC}⇒HK//OB (Quan hệ giữa tính vuông góc và tính song song của ba đường thẳng) (**)
Từ (*) và (**) ta có: MH và HK cùng thuộc một đường thẳng song song với OB.
Suy ra M, H, K thẳng hàng (điều phải chứng minh)
LT
17 tháng 3 2020
a) Xét tam giác AHO và tam giác BHO
có OH chung
HA=HB (GT)
OA=OB (GT)
suy ra tam giác AHO = tam giác BHO (c.c.c) (1)
b) Từ (1) suy ra góc AOC = góc BOC
Xét tam giác AOC và tam giác BOC có
OC chung
góc AOC = góc BOC
OA=OB (GT)
suy ra tam giác AOC = tam giác BOC (c.g.c)
suy ra góc OAC = góc OBC (hai góc tương ứng)
mà góc OAC =900
suy ra góc OBC = 900
suy ra CB vuông góc với OB tại B
Kẻ tia \(Ox//aa'\) (\(Ox\)nằm giữa \(OA\)và \(OB\))
\(Ox//aa'\)suy ra \(\widehat{a'AO}=\widehat{AOx}\)(hai góc so le trong)
\(\widehat{BOx}=\widehat{AOB}-\widehat{AOx}=68^o-40^o=28^o\)
Suy ra \(\widehat{BOx}=\widehat{OBb'}\)
mà hai góc này ở vị trí so le trong nên \(Ox//bb'\).
Suy ra \(aa'//bb'\).
\(OH\perp aa'\)suy ra \(OH\perp bb'\)vì \(aa'//bb'\).