Cho \(\Delta\)ABC vuông tại A, có AH là đường cao (AB<AC)
Chứng minh: \(AH^2=HB.HC\)
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
10 tháng 5 2023
a: Xét ΔHBA vuông tại H và ΔABC vuông tại A có
góc B chung
=>ΔHBA đồng dạng với ΔABC
MN
19 tháng 1 2021
\(Pytago:\)
\(AC^2=BC^2-AB^2\)
\(\Rightarrow AC=\sqrt{BC^2-AB^2}=\sqrt{5^2-4^2}=3\left(cm\right)\)
Áp dung HTL trong tam giác vuông ABC có :
\(AB\cdot AC=AH\cdot BC\\ \Leftrightarrow AH=\dfrac{AB\cdot AC}{BC}=\dfrac{3\cdot4}{5}=2.4\left(cm\right)\)
19 tháng 1 2021
Áp dụng định lí Pytago vào ΔABC vuông tại A, ta được:
\(AB^2+AC^2=BC^2\)
\(\Leftrightarrow AC^2=BC^2-AB^2=5^2-4^2=9\)
hay \(AC=\sqrt{9}=3cm\)
Áp dụng hệ thức lượng trong tam giác vuông vào ΔABC vuông tại A có AH là đường cao ứng với cạnh huyền BC, ta được:
\(AB\cdot AC=BC\cdot AH\)
\(\Leftrightarrow AH\cdot5=3\cdot4=12\)
hay AH=2,4cm
Vậy: AH=2,4cm
16 tháng 4 2021
a/ Xét \(\Delta ABC\) và \(\Delta HAC\) có :
\(\left\{{}\begin{matrix}\widehat{C}chung\\\widehat{BAC}=\widehat{AHC}=90^0\end{matrix}\right.\)
\(\Leftrightarrow\Delta ABC\sim HAC\left(g-g\right)\)
b/ \(BC=\sqrt{AB^2+AC^2}=10cm\)
\(AH.BC=AB.AC\Leftrightarrow AH=\dfrac{AB.AC}{BC}=4,8cm\)
c/ \(\Delta HEA\sim\Delta CEH\left(g-g\right)\)
\(\Leftrightarrow\dfrac{HE}{CE}=\dfrac{EA}{HE}\Leftrightarrow HE^2=EA.EC\left(đpcm\right)\)
16 tháng 4 2021
a) Xét ΔHAC và ΔABC có:
∠(ACH ) là góc chung
∠(BAC)= ∠(AHC) = 90o
⇒ ΔHAC ∼ ΔABC (g.g)
b) Xét ΔHAD và ΔBAH có:
∠(DAH ) là góc chung
∠(ADH) = ∠(AHB) = 90o
⇒ ΔHAD ∼ ΔBAH (g.g)
c) Tứ giác ADHE có 3 góc vuông ⇒ ADHE là hình chữ nhật.
⇒ ΔADH= ΔAEH ( c.c.c) ⇒ ∠(DHA)= ∠(DEA)
Mặt khác: ΔHAD ∼ ΔBAH ⇒ ∠(DHA)= ∠(BAH)
∠(DEA)= ∠(BAH)
Xét ΔEAD và ΔBAC có:
∠(DEA)= ∠(BAH)
∠(DAE ) là góc chung
ΔEAD ∼ ΔBAC (g.g)
d) ΔEAD ∼ ΔBAC
ΔABC vuông tại A, theo định lí Pytago:
Theo b, ta có:
25 tháng 3 2023
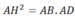
a)xét ΔABC và ΔHBA ta có
\(\widehat{BAH}=\widehat{BHA}=90^o\)
\(\widehat{B}chung\)
=>ΔABC ∼ ΔHBA(g.g)(1)
b)xét ΔABC và ΔAHC ta có
\(\widehat{BAC}=\widehat{AHC}=90^o\)
\(\widehat{B}chung\)
->ΔABC ∼ ΔAHC(g.g)(2)
từ (1) và (2)=>ΔHBA và ΔAHC
->\(\dfrac{AH}{BH}=\dfrac{HC}{AH}\)
=>\(AH^2=BH.HC\)
17 tháng 6 2017
1 / xét tam giác ABH đồng dạng vs CAH trg hợp g-g suy ra AB/AC =BH/AH
<=> 3 /7 =BH /42
=> BH =18 cm
2 áp dụng hệ thức lượng AH^2 =BH .CH từ bh/ch =9/16 =>CH= 16BH/9
TA CÓ AH ^2 =16BH^2 /9 SUY RA BH =36 cm SUY RA CH = 64 cm áp dụng pita go suy ra AB ,AC hoặc hệ thức lg cũng đc
2
8 tháng 5 2023
`a)` Xét `\triangle ABC` vuông tại `A` có: `\hat{B}+\hat{C}=90^o`
Xét `\triangle ABH` vuông tại `H` có: `\hat{B}+\hat{A_1}=90^o`
`=>\hat{C}=\hat{A_1}`
Xét `\triangle ABC` và `\triangle HBA` có:
`{:(\hat{C}=\hat{A_1}),(\hat{B}\text{ là góc chung}):}}=>\triangle ABC` $\backsim$ `\triangle HBA` (g-g)
`b)` Ta có: `BC=HB+HC=4+9=13(cm)`
Xét `\triangle ABC` vuông tại `A` có: `AH` là đường cao
`@AH=\sqrt{BH.HC}=6 (cm)`
`@AB=\sqrt{BH.BC}=2\sqrt{13}(cm)`
Ta có: `\hat{DEA}=\hat{ADH}=\hat{AEH}=90^o`
`=>` Tứ giác `AEHD` là hcn `=>DE=AH=6(cm)`
`c)` Xét `\triangle AHB` vuông tại `H` có: `HD \bot AB=>AH^2=AD.AB`
Xét `\triangle AHC` vuông tại `H` có: `HE \bot AC=>AH^2=AE.AC`
`=>AD.AB=AE.AC`
22 tháng 6 2023
2:
a: Xét ΔHAB vuông tại H và ΔHCA vuông tại H có
góc HAB=góc HCA
=>ΔHAB đồng dạng với ΔHCA
=>HA/HC=HB/HA
=>HA^2=HB*HC
b: BC=4+9=13cm
AH=căn 4*9=6cm
S ABC=1/2*6*13=39cm2
ta có: góc BAH + góc HAC = 90 độ
góc HCA + góc HAC = 90 độ
=> góc BAH = HCA
xét Tg ABH và Tg CAH
góc BHA = AHC = 90
góc BAH = HCA (cmt)
=> Tg ABH đồng dạng với Tg CAH (g.g)
=> BH/AH = AH/CH
nhân chéo => AH2 = BH.CH
mình xin lỗi vì đã quên nói nhưng bài này chưa được dùng tam giác đồng dạng