Cho a,b,c là các số thực thuộc đoạn [1,2 ].Chứng minh rằng:
\(\left(a+b+c\right)\left(\dfrac{1}{a}+\dfrac{1}{b}+\dfrac{1}{c}\right)\le10\)
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
20 tháng 3 2022
Bất đẳng thức sai, chẳng hạn với \(a=b=10^{-4};c=0,5-a-b\).
NV
Nguyễn Việt Lâm
Giáo viên
18 tháng 2 2022
Đặt \(a\left(1-b\right)=x;b\left(1-c\right)=y;c\left(1-a\right)=x\)
\(\Rightarrow1-\left(a+b+c\right)+ab+bc+ca=1-a\left(1-b\right)-b\left(1-c\right)-c\left(1-a\right)=1-x-y-z\)
BĐT cần c/m trở thành:
\(\dfrac{1}{x}+\dfrac{1}{y}+\dfrac{1}{z}\ge\dfrac{3}{1-x-y-z}\)
\(\Leftrightarrow\left(1-x-y-z\right)\left(\dfrac{1}{x}+\dfrac{1}{y}+\dfrac{1}{z}\right)-3\ge0\)
\(\Leftrightarrow\dfrac{1-x-y-z}{x}+\dfrac{1-x-y-z}{y}+\dfrac{1-x-y-z}{z}-3\ge0\)
\(\Leftrightarrow\dfrac{1-y-z}{x}+\dfrac{1-z-x}{y}+\dfrac{1-x-y}{z}-6\ge0\) (1)
Lại có: \(1-y-z=1-b\left(1-c\right)-c\left(1-a\right)=1-b-c+bc+ca=\left(1-b\right)\left(1-c\right)+ca\)
Nên (1) tương đương:
\(\dfrac{\left(1-b\right)\left(1-c\right)+ca}{a\left(1-b\right)}+\dfrac{\left(1-a\right)\left(1-c\right)+ab}{b\left(1-c\right)}+\dfrac{\left(1-a\right)\left(1-b\right)+bc}{c\left(1-a\right)}-6\ge0\)
\(\Leftrightarrow\dfrac{1-c}{a}+\dfrac{c}{1-b}+\dfrac{1-a}{b}+\dfrac{a}{1-c}+\dfrac{1-b}{c}+\dfrac{b}{1-a}\ge6\)
BĐT trên hiển nhiên đúng theo AM-GM do:
\(\dfrac{1-c}{a}+\dfrac{c}{1-b}+\dfrac{1-a}{b}+\dfrac{a}{1-c}+\dfrac{1-b}{c}+\dfrac{b}{1-a}\ge6\sqrt[6]{\dfrac{abc\left(1-a\right)\left(1-b\right)\left(1-c\right)}{abc\left(1-a\right)\left(1-b\right)\left(1-c\right)}}=6\) (đpcm)
Dấu "=" xảy ra khi \(a=b=c=\dfrac{1}{2}\)
19 tháng 2 2022
Cám ơn bài giải của thầy Lâm ạ!
Và từ bài bất đăng thức này, đã được chế thành bài toán hình học trong 1 kì thi học sinh giỏi toán cấp tỉnh thầy ạ!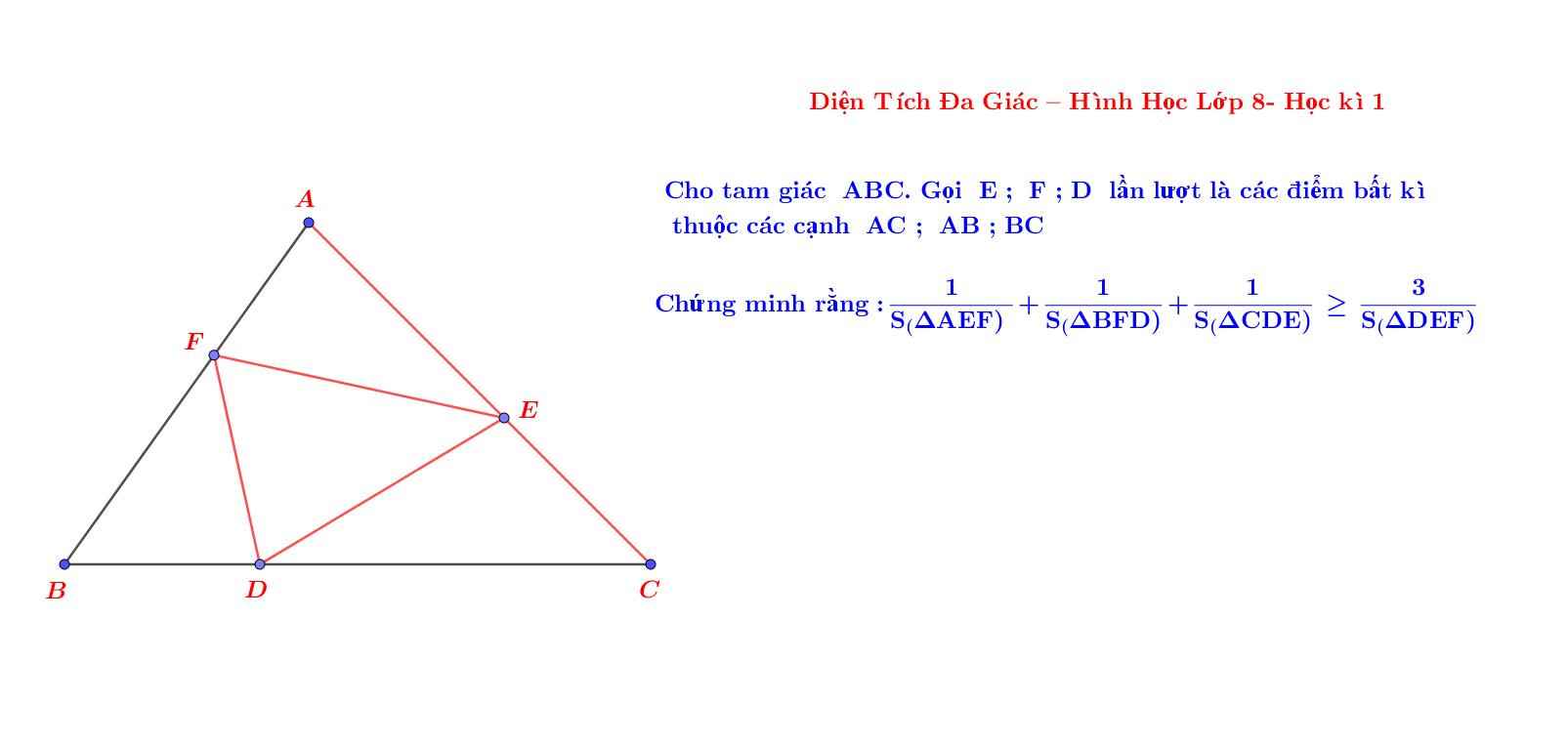
H
25 tháng 5 2023
Theo giả thiết kết hợp sử dụng BĐT AM - GM có:
\(\left(a+b-c\right)\left(\dfrac{1}{a}+\dfrac{1}{b}-\dfrac{1}{c}\right)=\left(a+b\right)\left(\dfrac{1}{a}+\dfrac{1}{b}\right)+1-\left[c\left(a+b\right)+c\left(\dfrac{1}{a}+\dfrac{1}{b}\right)\right]\)
\(\le\left(a+b\right)\left(\dfrac{1}{a}+\dfrac{1}{b}\right)+1-2\sqrt{\left(a+b\right)\left(\dfrac{1}{a}+\dfrac{1}{b}\right)}=\left[\sqrt{\left(a+b\right)\left(\dfrac{1}{a}+\dfrac{1}{b}\right)}-1\right]^2\)
Suy ra \(\sqrt{\left(a+b\right)\left(\dfrac{1}{a}+\dfrac{1}{b}\right)}-1\ge2\Leftrightarrow\sqrt{\dfrac{a}{b}+\dfrac{b}{a}+2}\ge3\)
\(\Leftrightarrow\dfrac{a}{b}+\dfrac{b}{a}\ge7\)
Khi đó, sử dụng BĐT Cauchy - Schwarz ta có:
\(\left(a^4+b^4+c^4\right)\left(\dfrac{1}{a^4}+\dfrac{1}{b^4}+\dfrac{1}{c^4}\right)\ge\left[\sqrt{\left(a^4+b^4\right)\left(\dfrac{1}{a^4}+\dfrac{1}{b^4}\right)}+1\right]^2\)
\(=\left(\dfrac{a^2}{b^2}+\dfrac{b^2}{a^2}+1\right)^2=\left[\left(\dfrac{a}{b}+\dfrac{b}{a}\right)^2-1\right]^2\ge\left(7^2-1\right)^2=2304\)
Đẳng thức xảy ra khi và chỉ khi \(ab=c^2\) và \(\dfrac{a}{b}+\dfrac{b}{a}=7\)
25 tháng 5 2023
(a+b-c)(1/a+1/b-c)=(a+b)(1/a+1/b)+1-[c(a+b)+c(1/a+1/b)]<=(a+b)(1/a+1/b)+1-2căn (a+b)(1/a+1/b)
=[(căn (a+b)(1/a+1/b))-1]^2
=>\(\sqrt{\left(a+b\right)\left(\dfrac{1}{a}+\dfrac{1}{b}\right)}-1>=2\)
=>\(\sqrt{\dfrac{a}{b}+\dfrac{b}{a}+2}>=3\)
=>a/b+b/a>=7
(a^4+b^4+c^4)(1/a^4+1/b^4+1/c^4)>=[căn ((a^4+b^4)(1/a^4+1/b^4))+1]^2
=(a^2/b^2+b^2/a^2+1)^2=[(a/b+b/a)^2-1]^2>=(7^2-1)^2=2304
=>ĐPCM
NV
Nguyễn Việt Lâm
Giáo viên
18 tháng 9 2021
\(\dfrac{a^3}{\left(b+1\right)\left(c+2\right)}+\dfrac{b+1}{12}+\dfrac{c+2}{18}\ge3\sqrt[3]{\dfrac{a^3\left(b+1\right)\left(c+2\right)}{216\left(b+1\right)\left(c+2\right)}}=\dfrac{a}{2}\)
Tương tự: \(\dfrac{b^3}{\left(c+1\right)\left(a+2\right)}+\dfrac{c+1}{12}+\dfrac{a+2}{18}\ge\dfrac{b}{2}\)
\(\dfrac{c^3}{\left(a+1\right)\left(b+2\right)}+\dfrac{a+1}{12}+\dfrac{b+2}{18}\ge\dfrac{c}{2}\)
Cộng vế:
\(VT+\dfrac{5}{36}\left(a+b+c\right)+\dfrac{7}{12}\ge\dfrac{1}{2}\left(a+b+c\right)\)
\(\Rightarrow VT\ge\dfrac{13}{36}\left(a+b+c\right)-\dfrac{7}{12}\ge\dfrac{13}{36}.3\sqrt[3]{abc}-\dfrac{7}{12}=\dfrac{1}{2}\) (đpcm)
NV
Nguyễn Việt Lâm
Giáo viên
10 tháng 4 2021
Không mất tính tổng quát, giả sử \(a\ge b\ge c\)
\(\Rightarrow P\le\dfrac{a}{b+c+1}+\dfrac{b}{b+c+1}+\dfrac{c}{b+c+1}+\left(1-a\right)\left(1-b\right)\left(1-c\right)\)
\(\Rightarrow P\le\dfrac{a+b+c}{b+c+1}+\left(1-a\right)\left(1-b\right)\left(1-c\right)=\dfrac{a-1}{b+c+1}+\left(1-a\right)\left(1-b\right)\left(1-c\right)+1\)
\(\Rightarrow P\le\left(1-a\right)\left[\left(1-b\right)\left(1-c\right)-\dfrac{1}{b+c+1}\right]+1\le\left(1-a\right)\left[\left(1-b\right)\left(1-c\right)-\dfrac{1}{bc+b+c+1}\right]+1\)
\(\Rightarrow P\le\left(1-a\right)\left[\left(1-b\right)\left(1-c\right)-\dfrac{1}{\left(1+b\right)\left(1+c\right)}\right]+1\)
\(\Rightarrow P\le\left(1-a\right)\left(\dfrac{\left(1-b^2\right)\left(1-c^2\right)-1}{\left(1+b\right)\left(1+c\right)}\right)+1\)
Do \(a;b;c\le1\Rightarrow\left\{{}\begin{matrix}1-a\ge0\\\left(1-b^2\right)\left(1-c^2\right)\le1\\\end{matrix}\right.\) \(\Rightarrow\left(1-a\right)\left[\dfrac{\left(1-b^2\right)\left(1-c^2\right)-1}{\left(1+b\right)\left(1+c\right)}\right]\le0\)
\(\Rightarrow P\le1\)
\(P_{max}=1\) khi \(\left(a;b;c\right)=\left(0;0;0\right);\left(1;1;1\right);\left(0;1;1\right);\left(0;0;1\right)\) và các hoán vị
NV
Nguyễn Việt Lâm
Giáo viên
30 tháng 8 2021
\(a+\dfrac{1}{a+1}=\dfrac{a^2+a+1}{a+1}=\dfrac{4a^2+4a+4}{4\left(a+1\right)}=\dfrac{3\left(a+1\right)^2+\left(a-1\right)^2}{4\left(a+1\right)}\ge\dfrac{3\left(a+1\right)^2}{4\left(a+1\right)}=\dfrac{3}{4}\left(a+1\right)\ge\dfrac{3}{2}\sqrt{a}\)
Tương tự: \(b+\dfrac{1}{b+1}\ge\dfrac{3}{2}\sqrt{b}\) ; \(c+\dfrac{1}{c+1}\ge\dfrac{3}{2}\sqrt{c}\)
Nhân vế:
\(VT\ge\dfrac{27}{8}\sqrt{abc}\ge\dfrac{27}{8}\) (đpcm)
Không mất tính tổng quát, giả sử \(a\ge b\ge c\).
Khi đó: \(\left(a-b\right)\left(b-c\right)\ge0\)
\(\Leftrightarrow ab+bc\ge ac+b^2\)
\(\Leftrightarrow\left\{{}\begin{matrix}\dfrac{a}{c}+1\ge\dfrac{a}{b}+\dfrac{b}{c}\\\dfrac{c}{a}+1\ge\dfrac{c}{b}+\dfrac{b}{a}\end{matrix}\right.\)
\(\Rightarrow\dfrac{a}{b}+\dfrac{b}{c}+\dfrac{c}{a}+\dfrac{b}{a}+\dfrac{c}{b}+\dfrac{a}{c}\le2+2\left(\dfrac{a}{c}+\dfrac{c}{a}\right)\)
Vì \(1\le c\le a\le2\Rightarrow\left(\dfrac{a}{c}-2\right)\left(\dfrac{2a}{c}-1\right)\le0\)
\(\Leftrightarrow\dfrac{a}{c}+\dfrac{c}{a}\le\dfrac{5}{2}\)
\(\Rightarrow\dfrac{a}{b}+\dfrac{b}{c}+\dfrac{c}{a}+\dfrac{b}{a}+\dfrac{c}{b}+\dfrac{a}{c}\le7\)
\(\Leftrightarrow\left(a+b+c\right)\left(\dfrac{1}{a}+\dfrac{1}{b}+\dfrac{1}{c}\right)\le10\)
Đẳng thức xảy ra khi \(a=b=2;c=1\) và các hoán vị.