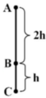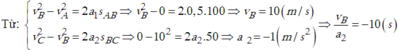Một thang máy chuyển động không vận tốc đầu từ mặt đất xuống một giếng sâu 150m. Trong 2/3 quãng đường đầu tiên, nó chuyển động với gia tốc không đổi 0.5m/s^2, trong 1/3 quãng đường còn lại nó chuyển...

TT

tien tran

29 tháng 9 2017

Một thang máy chuyển động không vận tốc đầu từ mặt đất xuống một giếng sâu 150m. Trong 2/3 quãng đường đầu tiên, nó chuyển động với gia tốc không đổi 0.5m/s^2, trong 1/3 quãng đường còn lại nó chuyển động chậm dần đều đến khi dừng hẳn ở đáy giếng. Tìm vận tốc cực đại của thang máy và gia tốc trên ở quãng đường...

Đọc tiếp

#Vật lý lớp 10

0

HD

Hoàng Đức Long

13 tháng 2 2018

Một thang máy chuyển động không vận tốc ban đầu từ mặt đất xuống một giếng sâu 150 m. Trong 2/3 quãng đường đầu tiên, thang có gia tốc 0,5 m/s2; trong 1/3 quãng đường sau, thang chuyển động chậm dần đều cho đến khi dừng hẳn ở đáy giếng. Vận tốc cực đại mà thnag máy đạt được là vmax và gia tốc thang máy trong giai đoạn sau là a2. Chọn chiều dương là chiều chuyển động. Độ lớn của...

Đọc tiếp

#Vật lý lớp 10

1

VT

Vũ Thành Nam

13 tháng 2 2018

Đúng(0)

HD

Hoàng Đức Long

18 tháng 6 2019

Một thang máy chuyển động không vận tốc ban đầu từ mặt đất xuống một giếng sâu 150 m. Trong 2/3 quãng đường đầu tiên, thang có gia tốc 0,5 m/s2; trong 1/3 quãng đường sau, thang chuyển động chậm dần đều cho đến khi dừng hẳn ở đáy giếng. Vận tốc cực đại mà thnag máy đạt được là vmax và gia tốc thang máy trong giai đoạn sau là a2. Chọn chiều dương là chiều chuyển động. Độ lớn của...

Đọc tiếp

#Vật lý lớp 10

1

VT

Vũ Thành Nam

18 tháng 6 2019

Chọn B.

Đúng(0)

NM

ng minh khôi

18 tháng 6 2023 - olm

Một xe máy chuyển động trong nửa thời gian đầu với vận tốc v1 =30km/h. Trong nửa thời gian còn lại thì nửa quãng đường đầu nó chuyển động với vận tốc v2= 45km/h, nửa quãng đường còn lại nó chuyển động với vận tốc v3. Biết rằng vận tốc trung bình của xe máy trên cả quãng đường là Vtb= 40km/h. Tính...

Đọc tiếp

#Vật lý lớp 8

1

H9

HT.Phong (9A5)

CTVHS

18 tháng 6 2023

Gọi s là độ dài nửa quãng đường. Ta có thời gian đi nửa quãng đường đầu là:

$t_1=\dfrac{s}{v_1}$

Gọi thời gian ô tô đi nửa phần còn lại là $t_2$ và $t_{3}$ và $t_2=t_3$

Thời gian ô tô đi được trong mỗi đoạn này là:

$s_2=v_2t_2$

$s_3=v_3t_3$

Mà: $t_2=t_3=\dfrac{s}{v_2+v_3}$

Vận tốc $v_3$ là:

$v_{tb}=\dfrac{2v_1\left(v_2+v_3\right)}{v_2+v_3+2v_1}$ hay $40=\dfrac{2\cdot30\cdot\left(45+v_3\right)}{45+v_3+2\cdot30}$

$\Leftrightarrow40=\dfrac{60\left(45+v_3\right)}{105+v_3}$

$\Leftrightarrow40\left(105+v_3\right)=60\left(45+v_3\right)$

$\Leftrightarrow2\left(105+v_3\right)=3\left(45+v_3\right)$

$\Leftrightarrow210+2v_3=135+3v_3$

$\Leftrightarrow3v_3-2v_3=210-135$

$\Leftrightarrow v_3=75\left(km/h\right)$

Đúng(2)

PT

Pham Trong Bach

6 tháng 8 2017

Một chiếc xe đua thể thức 1 bắt đầu chuyển động tăng tốc với gia tốc không đổi, khi vận tốc 80m/s thì xe chuyển động với vận tốc không đổi trong thời gian 56s, sau đó nó giảm với gia tốc không đổi đến khi dừng lại. Biết rằng thời gian chuyển động của xe là 74s. Tính quãng đường đi được của xe A. 5200 m B. 5500 m C. 5050 m D. 5350...

Đọc tiếp

#Mẫu giáo

1

CM

Cao Minh Tâm

6 tháng 8 2017

Đáp án A

Đúng(0)

NX

Nguyễn Xuân Tịnh

11 tháng 2 2019 - olm

Một chuyển động trong nửa đầu quãng đường chuyển động với vận tốc không đổi v1, trong nửa quãng đường còn lại có vận tốc v2.

Tính vận tốc trung bình của nó trên cả quãng đường . Chứng tỏ rằng vận tốc trung bình này không lớn hơn trung bình cộng của 2 vận tốc v1,v2.

😎 😎 😎 😎 😎

#Vật lý lớp 8

0

WR

wary reus

2 tháng 8 2016

Một chuyển động trong nửa đầu quãng đường , chuyển động có vận tốc không đổi V1 , trong nửa quãng đường còn lại có vận tốc V2 . Tính vận tốc trung bình của nó trên cả quãng đường . Chứng tỏ vận tốc trung bình này không lớn hơn trung bình cộng cảu hai vận tốc V1 và V2

#Vật lý lớp 8

1

TV

Truong Vu Xuan

2 tháng 8 2016

ta có:

t₁=$\frac{S_1}{v_1}=\frac{S}{2v_1}$

$t_2=\frac{S_2}{v_2}=\frac{S}{2v_2}$

vận tốc trung bình của nhười đó là:

$v_{tb}=\frac{S}{t_1+t_2}=\frac{S}{\frac{S}{2v_1}+\frac{S}{2v_2}}=\frac{1}{\frac{1}{2v_1}+\frac{1}{2v_2}}=\frac{1}{\frac{v_2+v_1}{2v_1v_2}}=\frac{2v_1v_2}{v_2+v_1}$

lấy v_tb-trung bình cộng 2 v ta có:

$\frac{2v_1v_2}{v_1+v_2}-\frac{v_1+v_2}{2}=\frac{4v_1v_2-v_1^2-2v_1v_2-v_2^2}{2\left(v_1+v_2\right)}=\frac{-\left(v_1^2-2v_1v_2+v_2^2\right)}{2\left(v_1+v_2\right)}$

$=\frac{-\left(v_1-v_2\right)^2}{2\left(v_1+v_2\right)}$

mà (v₁-v₂)²>0 nên

-(v₁-v₂)²<0 và 2*(v₂+v₁)>0 nên ta suy ra

vận tốc trung bình này ko bao giờ lớn hơn trung bình cộng của hai vận tốc v₁ và v₂

Đúng(0)

TH

Trang Heo

19 tháng 10 2020

cái chỗ vận tốc tb-tbc 2 v là 4v1v2- v1mũ 2 đúng ko

Đúng(0)

TN

Trần Ngọc Bảo Trân

25 tháng 7 2021

Một vật chuyển động hết quãng đường AB dài 180m. trong nữa đường đầu tiên nó đi với vận tốc v1-3m/s. Trong nữa đoạn đường sau nó đi với vận tốc v2 lớn gấp hai lần vận tốc v1. Tính thời gian chuyển động hết quãng đường

#Vật lý lớp 8

1

MY

missing you =

25 tháng 7 2021

$=>t1=\dfrac{\dfrac{1}{2}S}{v1}=\dfrac{\dfrac{1}{2}.180}{3}=30s$

$=>t2=\dfrac{\dfrac{1}{2}S}{2v1}=\dfrac{\dfrac{1}{2}.180}{6}=15s$

$=>t=t1+t2=45s$

Đúng(1)

KN

Kim Ngân

28 tháng 1 2021

Tính vận tốc trung bình trên toàn bộ quãng đường trong các trương hợp câu a và b sau:a) Một ô tô trong quãng đường đầu chuyển động với vận tốc không đổi v1, trong quãng đường còn lại chuyển động với vận tốc không đổi v2. Đáp án: 2v1.v2/(v1+v2)b) Một ô tô trong nửa thời gian đầu chuyển động với vận tốc không đổi v1, trong nửa thời gian còn lại chuyển động với vận tốc không đổi...

Đọc tiếp

#Vật lý lớp 8

0

M

M.Tuấn

18 tháng 9 2021

Một vật chuyển động trên đoạn đường AB dài 240 m. Trong 1 nửa đoạn đường đầu tiên nó chuyển động thẳng đều với vận tốc v1=5m/s, 1 nửa đoạn đường sau nó chuyển động thẳng đều với vận tốc v2=6m/s. Tính thời gian vật chuyển động hết quãng đường AB.

#Vật lý lớp 10

1

EC

Edogawa Conan

18 tháng 9 2021

Thời gian đi hết nửa quãng đường đầu là:

Ta có: $v_1=\dfrac{s_1}{t_1}\Leftrightarrow t_1=\dfrac{\dfrac{s}{2}}{v_1}=\dfrac{\dfrac{240}{2}}{5}=24\left(s\right)$

Thời gian đi hết nửa quãng đường sau là:

Ta có: $v_2=\dfrac{s_2}{t_2}\Leftrightarrow t_2=\dfrac{\dfrac{s}{2}}{v_2}=\dfrac{\dfrac{240}{2}}{6}=20\left(s\right)$

Thời gian đi hết quãng đường AB là:

$t_{AB}=t_1+t_2=24+20=44\left(s\right)$

Đúng(4)

Chúng tôi đề xuất

Tài nguyên

Ứng dụng mobile

Bảng xếp hạng

Các khóa học có thể bạn quan tâm

Yêu cầu VIP