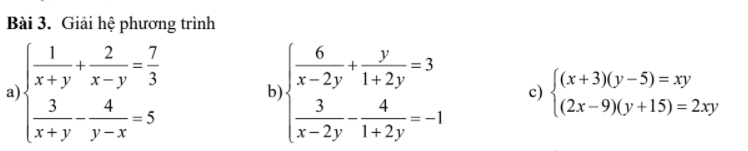Ai giúp em 10 với 8 được không ạ em cảm...
Đọc tiếp
Ai giúp em 10 với 8 được không ạ em cảm ơn!~
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
NR
Giúp em 7 8 10 được không ạ em cảm ơn
1
27 tháng 8 2021
10: Ta có: \(\left(\dfrac{x+1}{x}\right)^2:\left[\dfrac{x^2+1}{x^2}+\dfrac{2}{x+1}\cdot\left(\dfrac{1}{x+1}+1\right)\right]\)
\(=\dfrac{\left(x+1\right)^2}{x^2}:\left(\dfrac{x^2+1}{x^2}+\dfrac{2\cdot\left(x+2\right)}{\left(x+1\right)^2}\right)\)
\(=\dfrac{\left(x+1\right)^2}{x^2}:\dfrac{\left(x^2+1\right)\left(x^2+2x+1\right)+2x^2\left(x+2\right)}{x^2\left(x+1\right)^2}\)
\(=\dfrac{\left(x+1\right)^2}{x^2}\cdot\dfrac{x^2\left(x+1\right)^2}{x^4+2x^3+x^2+x^2+2x+1+2x^3+4x^2}\)
\(=\dfrac{\left(x+1\right)^4}{x^4+4x^3+6x^2+2x+1}\)
A
1
8 tháng 11 2021
8.
Gọi \(A\left(x_0;y_0\right)\) là điểm cố định mà đt luôn đi qua với mọi m
\(\Leftrightarrow mx_0+2y_0-3my_0+m-1=0\\ \Leftrightarrow m\left(x_0-3y_0+1\right)+\left(2y_0-1\right)=0\\ \Leftrightarrow\left\{{}\begin{matrix}x_0-3y_0+1=0\\2y_0-1=0\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x_0=\dfrac{1}{2}\\y_0=\dfrac{1}{2}\end{matrix}\right.\Leftrightarrow A\left(\dfrac{1}{2};\dfrac{1}{2}\right)\)
Vậy đt luôn đi qua \(A\left(\dfrac{1}{2};\dfrac{1}{2}\right)\) với mọi m
9.
PT giao Ox là \(y=0\Leftrightarrow mx+m-1=0\Leftrightarrow x=\dfrac{1-m}{m}\Leftrightarrow A\left(\dfrac{1-m}{m};0\right)\Leftrightarrow OA=\left|\dfrac{1-m}{m}\right|\)
PT giao Oy là \(x=0\Leftrightarrow\left(2-3m\right)y+m-1=0\Leftrightarrow y=\dfrac{1-m}{2-3m}\Leftrightarrow B\left(0;\dfrac{1-m}{2-3m}\right)\Leftrightarrow OB=\left|\dfrac{1-m}{2-3m}\right|\)
Để \(\Delta OAB\) cân thì \(OA=OB\Leftrightarrow\left|\dfrac{1-m}{m}\right|=\left|\dfrac{1-m}{2-3m}\right|\)
\(\Leftrightarrow\left|m\right|=\left|2-3m\right|\Leftrightarrow\left[{}\begin{matrix}m=2-3m\\m=3m-2\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}m=\dfrac{1}{2}\\m=1\end{matrix}\right.\)
Vậy \(\left[{}\begin{matrix}m=\dfrac{1}{2}\\m=1\end{matrix}\right.\) thỏa mãn đề
A
2
27 tháng 10 2021
Câu 7:
Thay x=0 và y=9 vào (d), ta được:
-2m-3=9
hay m=-6
A
0
A
0
5 tháng 12 2021
\(a,ĐK:x+y\ne0;x\ne y\\ HPT\Leftrightarrow\left\{{}\begin{matrix}\dfrac{2}{x+y}+\dfrac{4}{x-y}=\dfrac{14}{3}\left(1\right)\\\dfrac{3}{x+y}+\dfrac{4}{x-y}=5\left(2\right)\end{matrix}\right.\\ \left(2\right)-\left(1\right)=\dfrac{1}{x+y}=\dfrac{1}{3}\\ \Leftrightarrow x+y=3\\ \Leftrightarrow x=3-y\\ \text{Thay vào }\left(1\right)\Leftrightarrow\dfrac{2}{3}+\dfrac{4}{3-2y}=\dfrac{14}{3}\\ \Leftrightarrow\dfrac{4}{3-2y}=4\\ \Leftrightarrow3-2y=1\\ \Leftrightarrow y=1\Leftrightarrow x=2\)
Vậy hệ có nghiệm \(\left(x;y\right)=\left(2;1\right)\)
5 tháng 12 2021
\(b,ĐK:y\ne-\dfrac{1}{2};x-2y\ne0\\ HPT\Leftrightarrow\left\{{}\begin{matrix}\dfrac{6}{x-2y}+\dfrac{y}{1+2y}=3\left(1\right)\\\dfrac{6}{x-2y}-\dfrac{8}{1+2y}=-2\left(2\right)\end{matrix}\right.\\ \left(1\right)-\left(2\right)=\dfrac{y+8}{2y+1}=5\\ \Leftrightarrow y+8=10y+5\Leftrightarrow y=\dfrac{1}{3}\\ \text{Thay vào }\left(1\right)\Leftrightarrow\dfrac{6}{x-\dfrac{2}{3}}+\dfrac{\dfrac{1}{3}}{\dfrac{5}{3}}=3\\ \Leftrightarrow\dfrac{6}{x-\dfrac{2}{3}}=\dfrac{14}{5}\\ \Leftrightarrow x-\dfrac{2}{3}=\dfrac{15}{7}\Leftrightarrow x=\dfrac{59}{21}\)
Vậy hệ có nghiệm \(\left(x;y\right)=\left(\dfrac{59}{21};\dfrac{1}{3}\right)\)
18 tháng 8 2021
Bài 3:
a: \(1dm=\dfrac{1}{10}m\)
\(3dm=\dfrac{3}{10}m\)
\(9dm=\dfrac{9}{10}m\)
b: \(1g=\dfrac{1}{1000}kg\)
\(8g=\dfrac{1}{125}kg\)
\(25g=\dfrac{1}{40}kg\)
c: \(1'=\dfrac{1}{60}h\)
\(6'=\dfrac{1}{10}h\)
\(12'=\dfrac{1}{5}h\)
7 tháng 12 2021
\(12,ĐK:x,y\ne0\\ HPT\Leftrightarrow\left\{{}\begin{matrix}\dfrac{4}{x}+\dfrac{2}{y}=4\\\dfrac{6}{x}-\dfrac{2}{y}=1\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}\dfrac{10}{x}=5\\\dfrac{2}{x}+\dfrac{1}{y}=2\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x=2\\\dfrac{1}{y}=1\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x=2\\y=1\end{matrix}\right.\left(tm\right)\)
\(13,\Leftrightarrow\left\{{}\begin{matrix}3\left(x+1\right)+2\left(x+2y\right)=4\\8\left(x+1\right)-2\left(x+2y\right)=18\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}11\left(x+1\right)=22\\3\left(x+1\right)+2\left(x+2y\right)=4\end{matrix}\right.\\ \Leftrightarrow\left\{{}\begin{matrix}x=1\\6+2+4y=4\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x=1\\y=-1\end{matrix}\right.\)
\(14,ĐK:x+y\ne0;y\ne1\\ HPT\Leftrightarrow\left\{{}\begin{matrix}\dfrac{4}{x+y}+\dfrac{1}{y-1}=5\\\dfrac{4}{x+y}-\dfrac{8}{y-1}=-4\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}\dfrac{1}{x+y}-\dfrac{2}{y-1}=-1\\\dfrac{9}{y-1}=9\end{matrix}\right.\\ \Leftrightarrow\left\{{}\begin{matrix}\dfrac{1}{x+2}=1\\y=2\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x+2=1\\y=2\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x=-1\\y=2\end{matrix}\right.\left(tm\right)\)
\(15,ĐK:x\ge-1\\ HPT\Leftrightarrow\left\{{}\begin{matrix}2\left(x+y\right)+\sqrt{x+1}=4\\2\left(x+y\right)-6\sqrt{x+1}=-10\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}7\sqrt{x+1}=14\\2\left(x+y\right)+\sqrt{x+1}=4\end{matrix}\right.\\ \Leftrightarrow\left\{{}\begin{matrix}x=3\left(tm\right)\\6+2y+2=4\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x=3\\y=-2\end{matrix}\right.\left(tm\right)\)
7 tháng 12 2021
\(16,ĐK:x\ne1;y\ne-2\\ HPT\Leftrightarrow\left\{{}\begin{matrix}\dfrac{3x}{x-1}-\dfrac{2}{y+2}=4\\\dfrac{4x}{x-1}+\dfrac{2}{y+2}=10\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}\dfrac{7x}{x-1}=14\\\dfrac{2x}{x-1}+\dfrac{1}{y+2}=5\end{matrix}\right.\\ \Leftrightarrow\left\{{}\begin{matrix}x=2\\\dfrac{1}{y+2}=1\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x=2\\y=-1\end{matrix}\right.\left(tm\right)\)
\(17,ĐK:x\ge0;y\ge1\\ HPT\Leftrightarrow\left\{{}\begin{matrix}\sqrt{x}+2\sqrt{y-1}=5\\8\sqrt{x}-2\sqrt{y-1}=4\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}9\sqrt{x}=9\\\sqrt{x}+2\sqrt{y-1}=5\end{matrix}\right.\\ \Leftrightarrow\left\{{}\begin{matrix}x=1\\\sqrt{y-1}=2\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x=1\\y=5\end{matrix}\right.\)
\(18,\Leftrightarrow\left\{{}\begin{matrix}8x-2\left|y+2\right|=6\\x+2\left|y+2\right|=3\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}9x=9\\x+2\left|y+2\right|=3\end{matrix}\right.\\ \Leftrightarrow\left\{{}\begin{matrix}x=1\\\left|y+2\right|=1\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x=1\\\left[{}\begin{matrix}y=-1\\y=-3\end{matrix}\right.\end{matrix}\right.\\ 20,ĐK:y\ne1\\ HPT\Leftrightarrow\left\{{}\begin{matrix}2x+\dfrac{3}{y-1}=5\\12x-\dfrac{3}{y-1}=9\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}14x=14\\2x+\dfrac{3}{y-1}=5\end{matrix}\right.\\ \Leftrightarrow\left\{{}\begin{matrix}x=1\\\dfrac{3}{y-1}=3\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x=1\\y=2\end{matrix}\right.\left(tm\right)\)
\(21,ĐK:x\ne-1\\ HPT\Leftrightarrow\left\{{}\begin{matrix}\dfrac{9}{x+1}-6y=-3\\\dfrac{10}{x+1}+6y=22\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}\dfrac{19}{x+1}=19\\\dfrac{3}{x+1}-2y=-1\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x=0\\3-2y=-1\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x=0\\y=2\end{matrix}\right.\left(tm\right)\)
