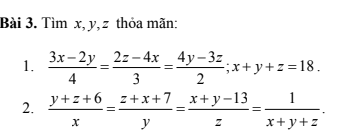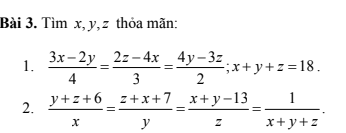Có bạn nào biết làm câu này ko thì giúp mình nha mình đang cần gấp trước 11 giờ, nếu được thì mình cảm ơn rất rất nhiều
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
30 tháng 8 2021
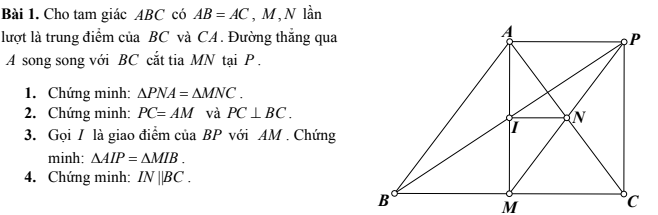
4: Xét ΔAMC có
I là trung điểm của AM
N là trung điểm của AC
Do đó: IN là đường trung bình của ΔAMC
Suy ra: IN//MC
hay IN//BC
31 tháng 8 2021
1: Xét ΔABC có AB=AC
nên ΔABC cân tại A
Suy ra: \(\widehat{B}=\widehat{C}\)
Ta có: ΔBAC cân tại A
mà AH là đường trung tuyến ứng với cạnh đáy BC
nên AH là đường cao ứng với cạnh BC
RH
30 tháng 8 2021
1. Tam giác AOC và tam giác BOD có: AO = BO; CO = DO: góc AOC = góc BOD (đối đỉnh)
--> tam giác AOC = tam giác BOD (c.g.c)
--> góc ACO = góc ODB
Mà 2 góc này ở vị trí so le trong
--> AC // BD
AH
Akai Haruma
Giáo viên
27 tháng 8 2021
Đây là bài bạn phải nộp cho thầy nên mình sẽ không làm chi tiết. Nhưng mình có thể gợi ý cho bạn như sau:
1.
Đối với tỉ lệ thức đã cho, mỗi phân số ta nhân cả tử và mẫu với 4, 3, 2. Khi đó, ta thu được 1 tỉ lệ thức mới
Dùng tỉ lệ thức trên, áp dụng tính chất dãy tỉ số bằng nhau (cộng), ta thu được $12x=8y=6z(*)$
Tiếp tục áp dụng tính chất dãy tỉ số bằng nhau cho $(*)$ dựa theo điều kiện $x+y+z=18$ ta sẽ tính được $x,y,z$ thỏa mãn.
AH
Akai Haruma
Giáo viên
27 tháng 8 2021
2.
Áp dụng tính chất dãy tỉ số bằng nhau (cộng) cho 3 phân số đầu tiên, ta sẽ tìm được tổng $x+y+z$
Khi tìm được tổng $x+y+z$, cộng vào 3 phân số đầu tiên trong bài, mỗi phân số cộng thêm 1. Khi đó, ta thu được tỉ lệ thức $\frac{m}{x}=\frac{n}{y}=\frac{p}{z}(*)$ với $m,n,p$ đã tính được dựa theo giá trị $x+y+z$.
Áp dụng tính chất dãy tỉ số bằng nhau cho tỉ lệ thức $(*)$, kết hợp với kết quả $x+y+z$ thì bài toán đã rất quen thuộc rồi.
NN
Nguyễn Ngọc Anh Minh
CTVHS
VIP
30 tháng 8 2021
1/
Xét tg ABC có AB=AC => tg ABC cân tại A \(\Rightarrow\widehat{B}=\widehat{C}\) (Trong tg cân hai góc ở đáy = nhau)
BH=CH => AH là đường trung tuyến \(\Rightarrow AH\perp BC\) (trong tg cân đường trung tuyến xp từ đỉnh đồng thời là đường cao và đường trung trực)
2/ Ta có
\(MN\perp BC;CP\perp BC\) => MN//CP
MN=CP
=> Tứ giác MNPC là hình bình hành (Tứ giác có cặp cạnh đối // và = nhau thì tứ giác đó là hbh)
=> MN=CP; MC=NP; MP chung \(\Rightarrow\Delta MCP=\Delta PMN\left(c.c.c\right)\)
3/
Trong hình bình hành MNPC thì MP và NC là hai đường chéo hbh
=> I là trung điểm của NC (trong hbh hai đường chéo cắt nhau tại trung điểm mỗi đường)
31 tháng 8 2021
1: Xét ΔABC có AB=AC
nên ΔABC cân tại A
Suy ra: \(\widehat{ABC}=\widehat{ACB}\)
Xét ΔABH và ΔACH có
AB=AC
AH chung
BH=CH
Do đó: ΔABH=ΔACH
Suy ra: \(\widehat{AHB}=\widehat{AHC}\)
mà \(\widehat{AHB}+\widehat{AHC}=180^0\)
nên \(\widehat{AHB}=\widehat{AHC}=\dfrac{180^0}{2}=90^0\)
Do đó: AH\(\perp\)BC