tìm x biết
5x . 5x+1 . 5x+2 <_ 1000000000000000000 : 218
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


a: =>2^4x<2^28
=>4x<28
=>x<7
b: =>5^3x+3<5
=>3x+3<1
=>3x<-2
=>x<-2/3

Bạn thử xem lại đề nhé, giữa 3 số này là dấu cộng hay dấu nhân.
Nếu là dấu cộng thì ta có:
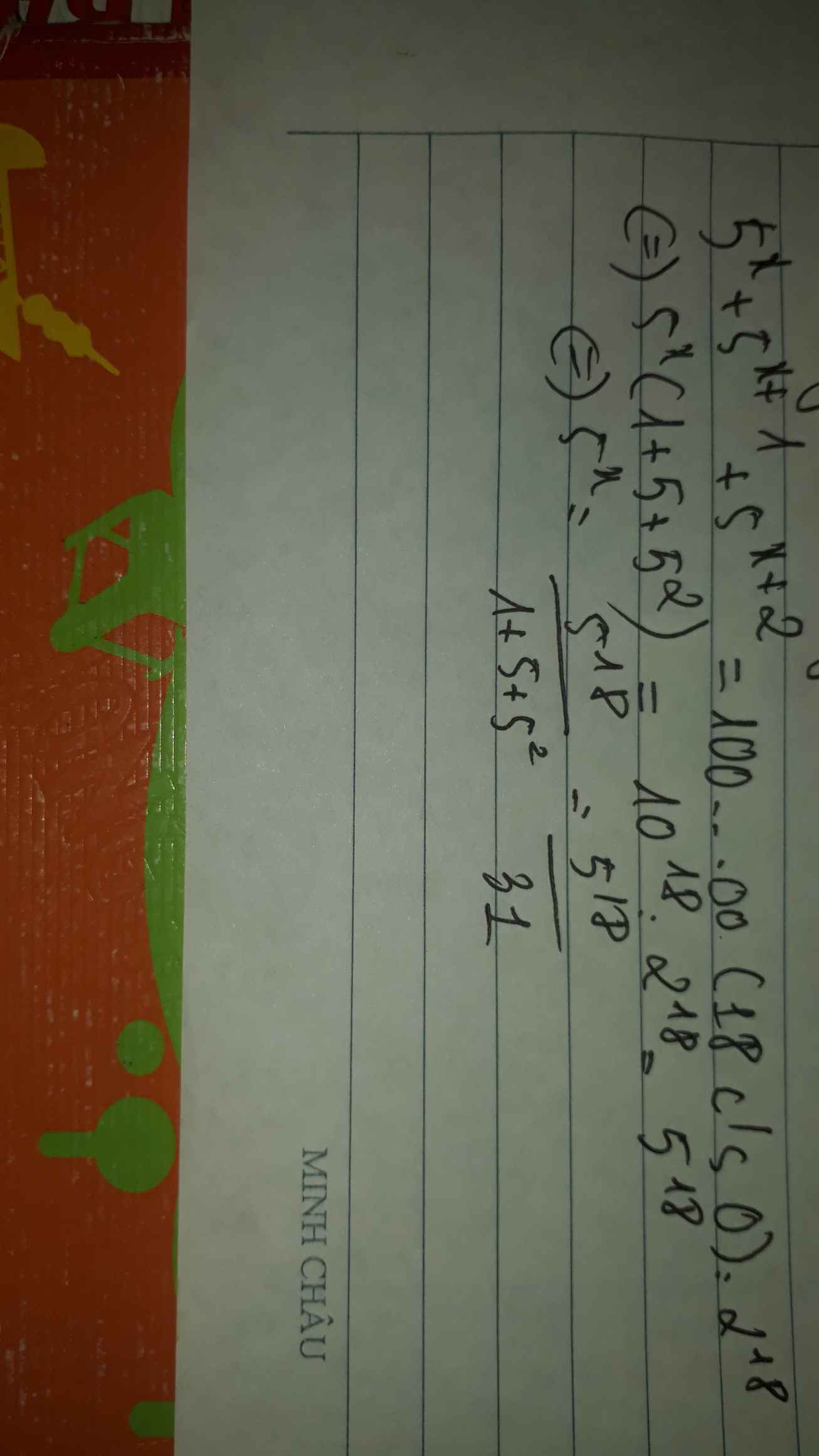
Nếu là dấu nhân thì ta có:


\(\left(5x+1\right)^2-\left(5x+3\right)\left(5x-3\right)=30\)
\(25x^2+10x+1-\left(25x^2-9\right)=30\)
\(25x^2+10x+1-25x^2+9=30\)
\(10x+10=30\)
\(10x=20\)
\(x=2\)

Bài làm:
a) \(x+5x^2=0\)
\(\Leftrightarrow x\left(1+5x\right)=0\)
\(\Leftrightarrow\orbr{\begin{cases}x=0\\1+5x=0\end{cases}\Rightarrow}\orbr{\begin{cases}x=0\\x=-\frac{1}{5}\end{cases}}\)
b) \(x\left(x-1\right)=x-1\)
\(\Leftrightarrow x^2-x-x+1=0\)
\(\Leftrightarrow x^2-2x+1=0\)
\(\Leftrightarrow\left(x-1\right)^2=0\)
\(\Rightarrow x-1=0\)
\(\Rightarrow x=1\)
c) \(5x\left(x-1\right)=1-x\)
\(\Leftrightarrow5x\left(x-1\right)+\left(x-1\right)=0\)
\(\Leftrightarrow\left(x-1\right)\left(5x+1\right)=0\)
\(\Leftrightarrow\orbr{\begin{cases}x-1=0\\5x+1=0\end{cases}}\Rightarrow\orbr{\begin{cases}x=1\\x=-\frac{1}{5}\end{cases}}\)
d) \(\left(3x-4\right)^2-\left(x+1\right)^2=0\)
\(\Leftrightarrow\left(2x-5\right)\left(4x-3\right)=0\)
\(\Leftrightarrow\orbr{\begin{cases}2x-5=0\\4x-3=0\end{cases}}\Rightarrow\orbr{\begin{cases}x=\frac{5}{2}\\x=\frac{3}{4}\end{cases}}\)
\(a,x+5x^2=0< =>x\left(5x+1\right)=0\)
\(< =>\orbr{\begin{cases}x=0\\5x+1=0\end{cases}< =>\orbr{\begin{cases}x=0\\5x=-1\end{cases}< =>\orbr{\begin{cases}x=0\\x=-\frac{1}{5}\end{cases}}}}\)
\(b,x\left(x-1\right)=x-1< =>x^2-x=x-1\)
\(< =>x^2-x-x+1=0< =>x\left(x-1\right)-\left(x-1\right)=0\)
\(< =>\left(x-1\right)\left(x-1\right)=0< =>x=1\)
\(c,5x\left(x-1\right)=1-x< =>5x^2-5x=1-x\)
\(< =>5x^2-5x+x-1=0< =>5x^2-4x-1=0\)
\(< =>5x^2-5x+x-1=0< =>5x\left(x-1\right)+x-1=0\)
\(< =>\left(5x+1\right)\left(x-1\right)=0< =>\orbr{\begin{cases}5x+1=0\\x-1=0\end{cases}}\)
\(< =>\orbr{\begin{cases}5x=-1\\x=1\end{cases}< =>\orbr{\begin{cases}x=-\frac{1}{5}\\x=1\end{cases}}}\)
\(d,\left(3x-4\right)^2-\left(x+1\right)^2=0\)
\(< =>9x^2-24x+16-x^2-2x-1=0\)
\(< =>8x^2-26x+15=0< =>8\left(x^2-\frac{13}{4}x+\frac{169}{64}\right)-\frac{2082}{64}=0\)
\(< =>\left(x-\frac{13}{8}\right)^2=\frac{2082}{512}=\frac{2082}{16\sqrt{2}}\)
\(< =>\orbr{\begin{cases}x-\frac{13}{8}=\frac{\sqrt{2082}}{4\sqrt[4]{2}}\\x-\frac{13}{8}=-\frac{\sqrt{2082}}{4\sqrt[4]{2}}\end{cases}}\)
\(< =>\orbr{\begin{cases}x=\frac{13}{8}+\frac{\sqrt{2082}}{4\sqrt[4]{2}}\\x=\frac{13}{8}-\frac{\sqrt{2082}}{4\sqrt[4]{2}}\end{cases}}\)(nghiệm vô tỉ)

a, \(-4x+5+2x-1=3\Leftrightarrow-2x=-1\Leftrightarrow x=\dfrac{1}{2}\)
b, \(-2x+2=2\Leftrightarrow x=0\)
c, \(-2x-6=-8\Leftrightarrow x=1\)

đặt biểu thức của bạn là A
Đê A <0 thì\(\orbr{\begin{cases}\left(\frac{2}{3}x-\frac{1}{5}\right)< 0;\left(\frac{3}{5}x+\frac{2}{3}\right)>0\\\left(\frac{2}{3}x-\frac{1}{5}\right)>0;\left(\frac{3}{5}x+\frac{2}{3}\right)< 0\end{cases}}\)
<=>\(\hept{\begin{cases}\frac{2}{3}x< \frac{1}{5};\frac{3}{2}x>\frac{-2}{3}\\\frac{2}{3}x>\frac{1}{5};\frac{3}{5}x< \frac{-2}{3}\end{cases}}\)(mình viết nhầm. Cái này là ngoặc vuông nhà)
<=> \(\orbr{\begin{cases}x< \frac{3}{10};x>\frac{-4}{9}\left(chon\right)\\x>\frac{3}{10};x< \frac{-4}{9}\left(loai\right)\end{cases}}\)
Vậy\(\frac{-4}{9}< x< \frac{3}{10}\)thì A<0