chứng minh rằng từ tỉ lệ thức \(\dfrac{a}{b}=\dfrac{c}{d}\) ( a#b ,c #d) ta có thể suy ra tỉ lệ thức \(\dfrac{a+b}{a-b}=\dfrac{c+d}{c-d}\)
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
HQ
Hà Quang Minh
Giáo viên
20 tháng 9 2023
a) Vì \(\dfrac{a}{b} = \dfrac{c}{d}\) nên \(ad = bc\)
Ta có \(\dfrac{{a + b}}{b} = \dfrac{{c + d}}{d}\)\( \Rightarrow d(a + b) = b(c + d)\)\( \Rightarrow ad + bd = bc + bd\)
\( \Rightarrow ad = bc\) (luôn đúng)
\( \Rightarrow \dfrac{{a + b}}{b} = \dfrac{{c + d}}{d}\)
b) Vì \(\dfrac{a}{b} = \dfrac{c}{d}\) nên \(ad = bc\)
Ta có: \(\dfrac{{a - b}}{b} = \dfrac{{c - d}}{d}\)
\(\begin{array}{l} \Rightarrow d(a - b) = b(c - d)\\ \Leftrightarrow ad - bd = bc - bd\\ \Leftrightarrow ad = bc\end{array}\) ( luôn đúng)
Vậy \(\dfrac{{a - b}}{b} = \dfrac{{c - d}}{d}\)
c) Vì \(\dfrac{a}{b} = \dfrac{c}{d}\) nên \(ad = bc\)
Ta có: \(\dfrac{a}{{a + b}} = \dfrac{c}{{c + d}}\)
\(\begin{array}{l} \Rightarrow a(c + d) = c(a + b)\\ \Leftrightarrow ac + ad = ac + bc\\ \Leftrightarrow ad = bc\end{array}\) (luôn đúng)
Vậy \(\dfrac{a}{{a + b}} = \dfrac{c}{{c + d}}\)
14 tháng 10 2021
a, Áp dụng t/c dtsbn:
\(\dfrac{a}{b}=\dfrac{c}{d}\Rightarrow\dfrac{a}{c}=\dfrac{b}{d}=\dfrac{a+b}{c+d}=\dfrac{a-b}{c-d}\Rightarrow\dfrac{a+b}{a-b}=\dfrac{c+d}{c-d}\)
b, Áp dụng t/c dtsbn:
\(\dfrac{a}{b}=\dfrac{c}{d}\Rightarrow\dfrac{a}{c}=\dfrac{b}{d}=\dfrac{2a}{2c}=\dfrac{5b}{5d}=\dfrac{3a}{4c}=\dfrac{4b}{4d}=\dfrac{2a+5b}{2c+5d}=\dfrac{3a-4b}{3c-4d}\Rightarrow\dfrac{2a+5b}{3a-4b}=\dfrac{2c+5d}{3c-4d}\)
14 tháng 10 2021
c, Đặt \(\dfrac{a}{b}=\dfrac{c}{d}=k\Rightarrow a=bk;c=dk\)
Ta có \(\dfrac{ab}{cd}=\dfrac{bk\cdot b}{dk\cdot d}=\dfrac{b^2k}{d^2k}=\dfrac{b^2}{d^2}\)
\(\dfrac{\left(a-b\right)^2}{\left(c-d\right)^2}=\dfrac{\left(bk-b\right)^2}{\left(dk-d\right)^2}=\dfrac{b^2\left(k-1\right)^2}{d^2\left(k-1\right)^2}=\dfrac{b^2}{d^2}\)
Do đó \(\dfrac{ab}{cd}=\dfrac{\left(a-b\right)^2}{\left(c-d\right)^2}\)
d, Đặt \(\dfrac{a}{b}=\dfrac{c}{d}=k\Rightarrow a=bk;c=dk\)
Ta có \(\dfrac{ac}{bd}=\dfrac{bk\cdot dk}{bd}=k^2\)
\(\dfrac{a^2+c^2}{b^2+d^2}=\dfrac{b^2k^2+d^2k^2}{b^2+d^2}=\dfrac{k^2\left(b^2+d^2\right)}{b^2+d^2}=k^2\)
Do đó \(\dfrac{ac}{bd}=\dfrac{a^2+c^2}{b^2+d^2}\)
HL
19 tháng 9 2017
Lần sau khi hỏi nhớ tìm xem có câu nào tương tự không nhé.
Ta có:
\(\dfrac{a}{b}=\dfrac{c}{d}\Leftrightarrow\dfrac{a}{c}=\dfrac{b}{d}=\dfrac{a+b}{c+d}=\dfrac{a-b}{c-d}\)
\(\Rightarrow\dfrac{a+b}{a-b}=\dfrac{c+d}{c-d}\)
Vậy nếu \(\dfrac{a}{b}=\dfrac{c}{d}\) ( a khác b, c khác d ) thì \(\dfrac{a+b}{a-b}=\dfrac{c+d}{c-d}\)
4 tháng 10 2023
Ta đặt:
\(\dfrac{a}{b}=\dfrac{c}{d}=k\) => \(a=b\times k\) ; \(c=d\times k\)
a) Ta có: \(\dfrac{a}{b}=\dfrac{b\times k}{d\times k}=\dfrac{b}{d}\) (1)
=> \(\dfrac{a+b}{c+d}=\dfrac{b\times k+b}{d\times k+d}=\dfrac{b\times\left(k+1\right)}{d\times\left(k+1\right)}=\dfrac{b}{d}\) (2)
Từ (1),(2) => đpcm
b)
\(\dfrac{a+b}{a}=\dfrac{b\times k+b}{b\times k}=\dfrac{b\times\left(k+1\right)}{b\times k}=\dfrac{k+1}{k}\) (1)
\(\dfrac{c+d}{c}=\dfrac{d\times k+d}{d\times k}=\dfrac{d\times\left(k+1\right)}{d\times k}=\dfrac{k+1}{k}\) (2)
Từ (1),(2) => đpcm
LH
18 tháng 4 2017
Ta có : \(\dfrac{a}{b}=\dfrac{c}{d}\) suy ra \(\dfrac{a}{c}=\dfrac{b}{d}\)
Theo tính chất dãy tỉ số bằng nhau ta có
\(\dfrac{a}{c}=\dfrac{b}{d}=\dfrac{a+b}{c+d}=\dfrac{a-b}{c-d}\)
Suy ra: \(\dfrac{a+b}{a-c}=\dfrac{c+d}{c-d}\)
TN
11 tháng 7 2017
Đặt \(\dfrac{a}{b}=\dfrac{c}{d}=k\)
\(\Rightarrow a=bk\) và \(c=dk\)
Nên \(\dfrac{a+b}{c-d}=\dfrac{bk+b}{dk-d}=\dfrac{b\left(k+1\right)}{d\left(k-1\right)}=\dfrac{k+1}{k-1}\)
\(\dfrac{c+d}{c-d}=\dfrac{dk+d}{dk-d}=\dfrac{d\left(k+1\right)}{d\left(k-1\right)}=\dfrac{k+1}{k-1}\)
\(\Rightarrow\dfrac{a+b}{c-d}=\dfrac{c+d}{c-d}\) (với \(a-b\ne0,c-d\ne0\))
Vậy \(\dfrac{a}{b}=\dfrac{c}{d}thì\)\(\dfrac{a+b}{c-d}=\dfrac{c+d}{c-d}\) ( \(a-b\ne0,c-d\ne0\))
14 tháng 7 2021
\(\dfrac{a}{b}=\dfrac{c}{d}=>\dfrac{a}{b}+1=\dfrac{c}{d}+1=>\dfrac{a+b}{b}=\dfrac{c+d}{d}\)
\(\dfrac{a}{b}=\dfrac{c}{d}=>\dfrac{a}{b}-1=\dfrac{c}{d}-1=>\dfrac{a-b}{b}=\dfrac{c-d}{d}\)
\(\dfrac{a}{b}=\dfrac{c}{d}=>ad=cb=>ad+ac=cb+ac\)
\(=>a\left(c+d\right)=c\left(a+b\right)=>\dfrac{a}{c}=\dfrac{a+b}{c+d}=>\dfrac{a}{a+b}=\dfrac{c}{c+d}\)
5 tháng 1 2022
\(\Leftrightarrow\dfrac{a+b}{c+d}=\dfrac{a-b}{c-d}=\dfrac{a}{c}=\dfrac{b}{d}=>\dfrac{a}{b}=\dfrac{c}{d}\)
AH
Akai Haruma
Giáo viên
5 tháng 1 2022
Lời giải:
$\frac{a+b}{a-b}=\frac{c+d}{c-d}$
$\Rightarrow (a+b)(c-d)=(a-b)(c+d)$
$\Rightarrow ac-ad+bc-bd=ac+ad-bc-bd$
$\Rightarrow 2ad=2bc$
$\Rightarrow ad=bc$
$\Rightarrow \frac{a}{b}=\frac{c}{d}$ (đpcm)
22 tháng 4 2018
a, ta có :
\(\dfrac{a}{b}=\dfrac{c}{d}=\dfrac{a}{c}=\dfrac{b}{d}=\dfrac{2a}{2c}=\dfrac{2b}{2d}\)
áp dụng tính chất dă y tỉ số bằng nhau ta có:
\(\dfrac{a}{b}=\dfrac{c}{d}=\dfrac{a}{c}=\dfrac{b}{d}=\dfrac{2a}{2c}=\dfrac{2b}{2d}=\dfrac{a+2b}{c+2d}=\dfrac{2a-b}{2c-d}\)
\(\Rightarrow\dfrac{a+2b}{c+2d}=\dfrac{2a-b}{2c-d}\Rightarrow\dfrac{a+2b}{2a-b}=\dfrac{c+2d}{2c-d}\) (ĐPCM)
22 tháng 4 2018
b, ta có:
\(\dfrac{a}{b}=\dfrac{c}{d}=\dfrac{3c}{3d}\)
áp dụng tính chất dă tỉ số bằng nhau ta có :
\(\dfrac{a}{b}=\dfrac{c}{d}=\dfrac{3c}{3d}=\dfrac{a+3c}{b+3d}=\dfrac{a-c}{b-d}\)
\(\Rightarrow\dfrac{a+3c}{b+3d}=\dfrac{a-c}{b-d}\)
\(\Rightarrow\left(a+3c\right)\left(b-d\right)=\left(b+3d\right)\left(a-c\right)\) (ĐPCM)
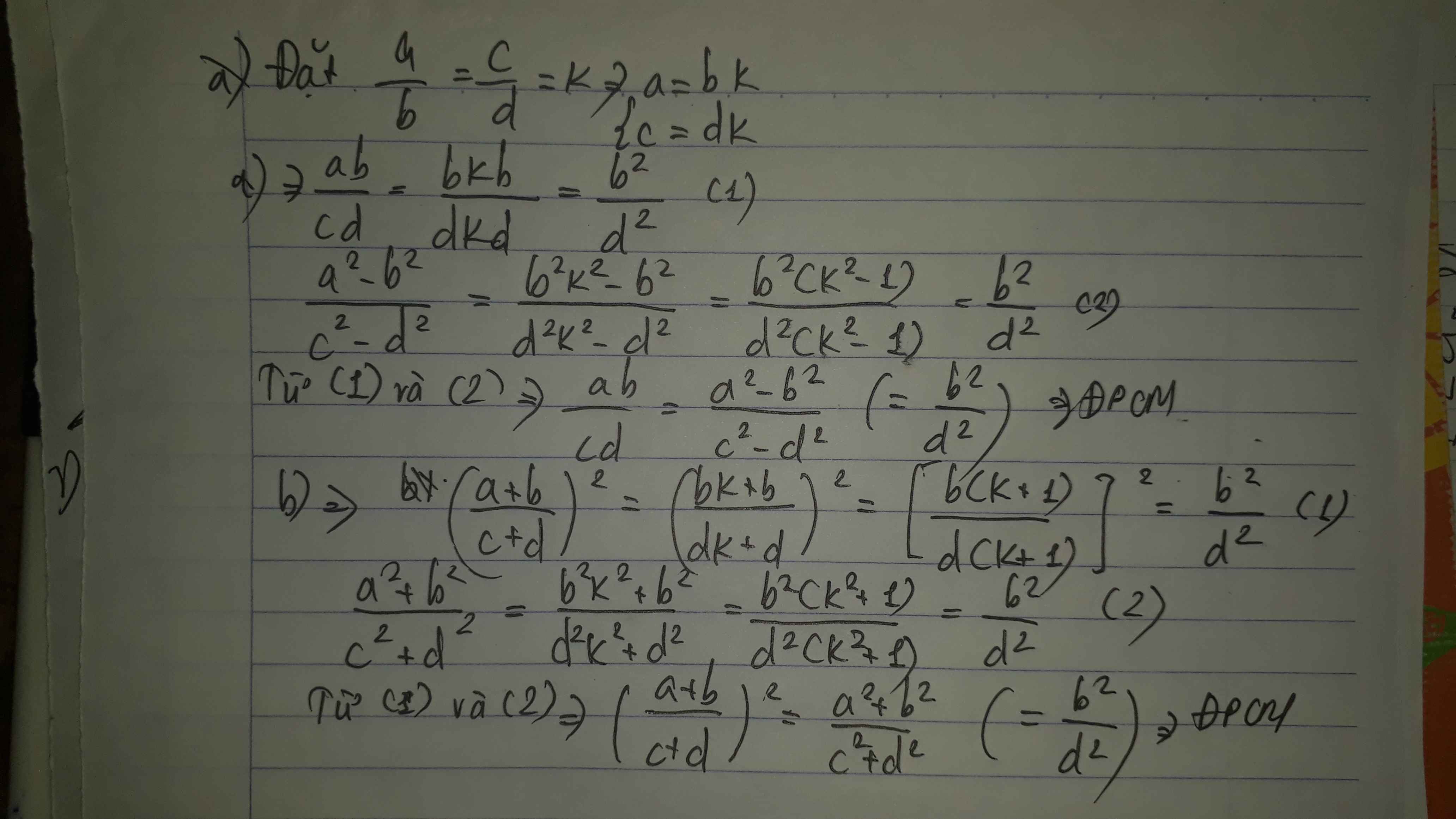
Đặt \(\dfrac{a}{b}=\dfrac{c}{d}=k\)
\(\Rightarrow a=bk,c=dk\)
Ta có: \(\dfrac{a+b}{a-b}=\dfrac{bk+b}{bk-b}=\dfrac{b\left(k+1\right)}{b\left(k-1\right)}=\dfrac{k+1}{k-1}\) (1)
\(\dfrac{c+d}{c-d}=\dfrac{dk+d}{dk-d}=\dfrac{d\left(k+1\right)}{d\left(k-1\right)}=\dfrac{k+1}{k-1}\) (2)
Từ (1) và (2) \(\Rightarrow\dfrac{a+b}{a-b}=\dfrac{c+d}{c-d}\)
Ta có: \(\dfrac{a}{b}\)=\(\dfrac{c}{d}\).Theo tính chất của dãy tỉ số bằng nhau:
\(\Rightarrow\)\(\dfrac{a}{b}\)=\(\dfrac{c}{d}\)=\(\dfrac{a+b}{c+d}\)=\(\dfrac{a-b}{c-d}\)
Vì \(\dfrac{a+b}{c+d}\)=\(\dfrac{a-b}{c-d}\)\(\Leftrightarrow\)\(\dfrac{a+b}{a-b}\)=\(\dfrac{c+d}{c-d}\)
Vậy \(\dfrac{a+b}{a-b}\)=\(\dfrac{c+d}{c-d}\)
Nếu bạn muốn làm cách cơ bản thì hãy làm theo mình.Còn nếu bạn học toán nâng cao thì làm theo cách bạn Linh hay hơn.Chúc bạn học tốt