1. Tìm giá trị nhỏ nhất:
E=I4x-3I + I5y + 7,5I + 17,5
2. Tìm giá trị lớn nhất:
F= 4-I5x-2I - I3x+12I ("I" là dấu giá trị tuyệt đối nha)
CẦN GẤP CẦN GẤP!!!!!!!
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

\(C=\left|4x-3\right|+\left|5y+7,5\right|+17,5\)
Có: \(\left|4x-3\right|\ge0\forall x\in R\)
\(\left|5y+7,5\right|\ge0\forall x\in R\)
\(\Rightarrow\left|4x-3\right|+\left|5y+7,5\right|\ge0\forall x\in R\)
\(\Rightarrow\left|4x-3\right|+\left|5y+7,5\right|+17,5\ge17,5\forall x\in R\)
\(\Rightarrow C\ge17,5\forall x\in R\)
Đẳng thức xảy ra \(\Leftrightarrow\hept{\begin{cases}\left|4x-3\right|=0\\\left|5y+7,5\right|=0\end{cases}}\Rightarrow\hept{\begin{cases}4x-3=0\\5y+7,5=0\end{cases}}\Rightarrow\hept{\begin{cases}4x=3\\5y=-7,5\end{cases}}\Rightarrow\hept{\begin{cases}x=0,75\\y=-1,5\end{cases}}\)
Vậy GTNN của C = 17,5 \(\Leftrightarrow\left(x;y\right)=\left(0,75;-1,5\right)\)
\(C=|4x-3|+|5y+7,5|+17,5\)
Có: \(|4x-3|\ge0\forall x\in R\)
\(|5y+7,5|\ge0\forall x\in R\)
\(\Rightarrow|4x-3|+|5y+7,5|\ge0\forall x\in R\)
\(\Rightarrow|4x-3|+|5y+7,5|+17,5\ge17,5\forall x\in R\)
\(\Rightarrow C\ge17,5\forall x\in R\)
Đẳng thức xảy ra khi \(\Leftrightarrow\hept{\begin{cases}|4x-3|=0\\|5y+7,5|=0\end{cases}\Rightarrow\hept{\begin{cases}4x-3=0\\5y+7,5=0\end{cases}\Rightarrow}\hept{\begin{cases}4x=3\\5y=-7,5\end{cases}\Rightarrow}\hept{\begin{cases}x=0,75\\y=-1,5\end{cases}}}\)
Vậy GTNN của \(C=17,5\Leftrightarrow\left(x;y\right)=\left(0,75;-1,5\right)\)


*\(x\ge\dfrac{1}{2}\Leftrightarrow\left|2x-1\right|=2x-1\)
\(D=\left(2x-1\right)^2-3\left(2x-1\right)+2=\left(2x-1\right)^2-2.\dfrac{3}{2}\left(2x-1\right)+\dfrac{9}{4}-\dfrac{1}{4}=\left(2x-1-\dfrac{3}{2}\right)^2-\dfrac{1}{4}=\left(2x-\dfrac{5}{2}\right)^2-\dfrac{1}{4}\ge-\dfrac{1}{4}\)\(D_{min}=-\dfrac{1}{4}\Leftrightarrow x=\dfrac{5}{4}\left(1\right)\)
*\(x< \dfrac{1}{2}\Leftrightarrow\left|2x-1\right|=-2x+1\)
\(D=\left(2x-1\right)^2+3\left(2x-1\right)+2=\left(2x-1\right)^2+2.\dfrac{3}{2}\left(2x-1\right)+\dfrac{9}{4}-\dfrac{1}{4}=\left(2x-1+\dfrac{3}{2}\right)^2-\dfrac{1}{4}=\left(2x+\dfrac{1}{2}\right)^2-\dfrac{1}{4}\ge-\dfrac{1}{4}\)\(D_{min}=-\dfrac{1}{4}\Leftrightarrow x=\dfrac{-1}{4}\left(2\right)\)
-Từ (1) và (2) suy ra \(D_{min}=-\dfrac{1}{4}\Leftrightarrow x\in\left\{\dfrac{5}{4};\dfrac{-1}{4}\right\}\)

a) TH1: Với \(x< 0\) thì \(\left|2x+3\right|=-\left(2x+3\right)=-2x-3\)
TH2: Với \(x\ge0\) thì \(\left|2x+3\right|=2x+3\)
b) TH1: Với \(x< 0\) thì \(\left|4x-2\right|=-\left(4x-2\right)=-4x+2\)
TH2: Với \(x\ge0\) thì \(\left|4x-2\right|=4x-2\)
c) TH1: Với \(x< 0\) thì \(\left|3x-5\right|=-\left(3x-5\right)=-3x+5\)
TH2: Với \(x\ge0\) thì \(\left|3x-5\right|=3x-5\)
a: TH1: x>=-3/2
=>A=2x+3
TH2: x<-3/2
=>A=-2x-3
b: TH1: x>=1/2
=>A=4x-2
TH2: x<1/2
=>A=-4x+2
c: TH1: x>=5/3
=>B=5x-3
TH2: x<5/3
=>B=-5x+3

\(\Leftrightarrow\orbr{\begin{cases}x\cdot\left(x-3\right)=x\\x\cdot\left(x-3\right)=-x\end{cases}}\Leftrightarrow\orbr{\begin{cases}x-3=\frac{x}{x}\\x-3=-\frac{x}{x}\end{cases}\Leftrightarrow\orbr{\begin{cases}x-3=1\\x-3=-1\end{cases}\Leftrightarrow}\orbr{\begin{cases}x=1+3\\x=-1+3\end{cases}}}\)
\(\Leftrightarrow\orbr{\begin{cases}x=4\\x=2\end{cases}}\)
Vậy x=2 hoặc x=4

4. A=7-x/x-5=(-(x-5)+2)/x-5=-1+2/x-5
A nhỏ nhất khi 2/x-5 nhỏ nhất.mà 2/x-5 nho nhất khi x-5 lớn nhất(a)
TH1: x-5>0=>x>5=>2/x-5>0(1)
Th2:x-5<0=>x<5=>2/x-5<0(2)
(1), (2)=>x-5<0(b)
(a),(b)=>x-5=-1=>x=4
vậy A nhỏ nhất là -3


Chọn D.
Ta có P = |2z + 1 = 2i| nên 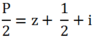
Ta cần tìm giá trị lớn nhất, giá trị nhỏ nhất của: 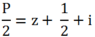
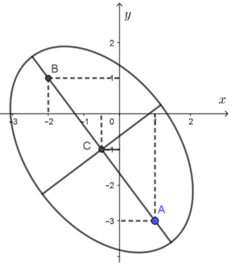
Ta có z1 = 1 - 3i; z2 = -2 + i và z0 = -1/2 - i
Ta thấy: ![]()
Tính 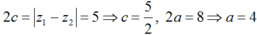
Suy ra 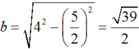
Vậy Max P = 2.4 = 8 và 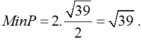

Chọn B.
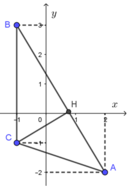
Gọi M (x; y) là điểm biểu diễn của số phức z trên mặt phẳng Oxy.
Gọi điểm A(2; -2) ; B(-1; 3) và C(-1; -1)
Phương trình đường thẳng AB: 5x + 3y - 4 = 0.
Khi đó theo đề bài ![]()
Ta có ![]() . Do đó quỹ tích M là đoạn thẳng AB.
. Do đó quỹ tích M là đoạn thẳng AB.
Tính CB = 4 và ![]() .
.
Hình chiếu H của C trên đường thẳng AB nằm trên đoạn AB.
Vậy 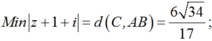
![]()
1/ Ta có :
\(E=\left|4x-3\right|+\left|5y+7,5\right|+17,5\)
Mà \(\left\{{}\begin{matrix}\left|4x-3\right|\ge0\\\left|5y+7,5\right|\ge0\end{matrix}\right.\)
\(\Leftrightarrow E=\left|4x-3\right|+\left|5y+7,5\right|+17,5\ge17,5\)
Để E đạt GTNN thì \(\left\{{}\begin{matrix}\left|4x-3\right|\\\left|5y+7,5\right|\end{matrix}\right.\) đạt GTNN
Dấu "=" xảy ra khi :
\(\left\{{}\begin{matrix}\left|4x-3\right|=0\\\left|5y+7,5\right|=0\end{matrix}\right.\) \(\Leftrightarrow\left\{{}\begin{matrix}4x-3=0\\5y+7,5=0\end{matrix}\right.\) \(\Leftrightarrow\left\{{}\begin{matrix}x=0,75\\y=-1,5\end{matrix}\right.\)
Vậy GTNN của E bằng 17,5 khi \(\left\{{}\begin{matrix}x=0,75\\y=-1,5\end{matrix}\right.\)
Bài 2?!?