Giúp em chi tiết câu này vs 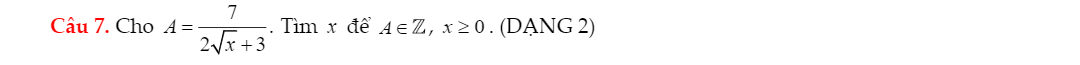
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Để \(P\in Z\) thì
\(\sqrt{x}-2\inƯ\left(5\right)=\left\{1;-1;5;-5\right\}\)
Mà \(x\in N,x\ne4\)
\(\Rightarrow x\in\left\{9;1;49\right\}\)
Vậy giá trị x lớn nhất cần tìm là: x=49

\(A=\dfrac{\sqrt{x}+1}{\sqrt{x}-1}=\dfrac{\sqrt{x}-1}{\sqrt{x}-1}+\dfrac{2}{\sqrt{x}-1}=1+\dfrac{2}{\sqrt{x}-1}\)
Để \(A\in Z\) thì \(\sqrt{x}-1\inƯ\left(2\right)=\left\{1;-1;2;-2\right\}\)
Mà \(x\in Z,x\ge0,x\ne1\)
\(\Rightarrow x\in\left\{4;0;9\right\}\)

\(M=\dfrac{\sqrt{x}+3}{\sqrt{x}-3}\left(đk:x\ge0,x\ne9\right)\)
Để \(M=\dfrac{\sqrt{x}+3}{\sqrt{x}-3}< 0\) thì
\(\sqrt{x}-3< 0\) ( do \(\sqrt{x}+3\ge3>0\))
\(\Leftrightarrow\sqrt{x}< 3\Leftrightarrow0\le x< 9\)
Mà \(x\in Z\)
\(\Rightarrow x\in\left\{0;1;2;3;4;5;6;7;8\right\}\)

\(1,\\ a,=6x^4y^4-x^3y^3+\dfrac{1}{2}x^4y^2\\ b,=4x^3+5x^2-8x^2-10x+12x+15\\ =4x^3-3x^2+2x+15\\ 2,\\ a,=7\left(x^2-6x+9\right)=7\left(x-3\right)^2\\ b,=\left(x-y\right)^2-36=\left(x-y-6\right)\left(x-y+6\right)\\ 3,\\ \Leftrightarrow x\left(x^2-0,36\right)=0\\ \Leftrightarrow x\left(x-0,6\right)\left(x+0,6\right)=0\\ \Leftrightarrow\left[{}\begin{matrix}x=0\\x=0,6\\x=-0,6\end{matrix}\right.\)

ĐK: \(x\ge0;x\ne\dfrac{1}{4}\)
\(A=\dfrac{4\sqrt{x}+3}{2\sqrt{x}-1}\in Z\)
\(\Leftrightarrow\dfrac{2\left(2\sqrt{x}-1\right)+5}{2\sqrt{x}-1}\in Z\)
\(\Leftrightarrow2+\dfrac{5}{2\sqrt{x}-1}\in Z\)
\(\Leftrightarrow2\sqrt{x}-1\inƯ_5=\left\{\pm1;\pm5\right\}\)
\(\Leftrightarrow2\sqrt{x}\in\left\{0;2;6\right\}\)
\(\Leftrightarrow\sqrt{x}\in\left\{0;1;3\right\}\)
\(\Leftrightarrow x\in\left\{0;1;9\right\}\)
Để A là số nguyên thì \(4\sqrt{x}+3⋮2\sqrt{x}-1\)
\(\Leftrightarrow5⋮2\sqrt{x}-1\)
\(\Leftrightarrow2\sqrt{x}-1\in\left\{-1;1;5\right\}\)
\(\Leftrightarrow2\sqrt{x}\in\left\{0;2;6\right\}\)
hay \(x\in\left\{0;1;9\right\}\)


24.
Đường thẳng có 1 vtcp là \(\overrightarrow{u}=\left(2;-5\right)\)
25.
\(a^2=b^2+c^2-2bc.cosA\)
26.
A là mệnh đề sai, công thức đúng: \(S=\dfrac{1}{2}ab.sinC\)
27.
\(BC=\sqrt{AB^2+AC^2-2AB.AC.cosA}=\sqrt{3^2+4^2-2.3.4.cos60^0}=\sqrt{13}\)
28.
\(\widehat{A}=180^0-\left(35^030'+45^0\right)=99^030'\)
Áp dụng định lý hàm sin:
\(\dfrac{a}{sinA}=\dfrac{b}{sinB}\Rightarrow b=\dfrac{a.sinB}{sinA}=\dfrac{12,5.sin\left(35^030'\right)}{sin\left(99^030'\right)}=7,36\left(m\right)\)

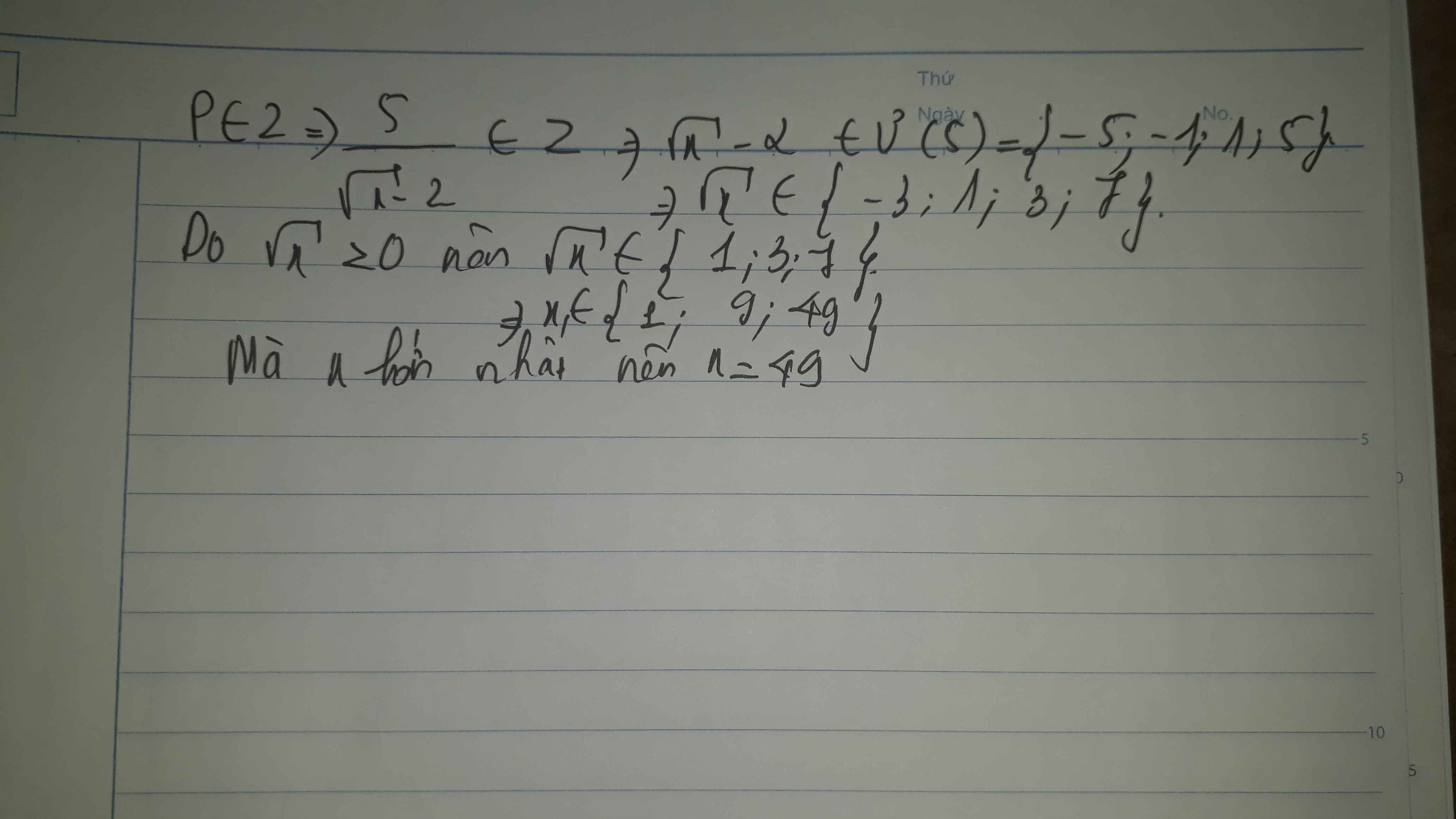

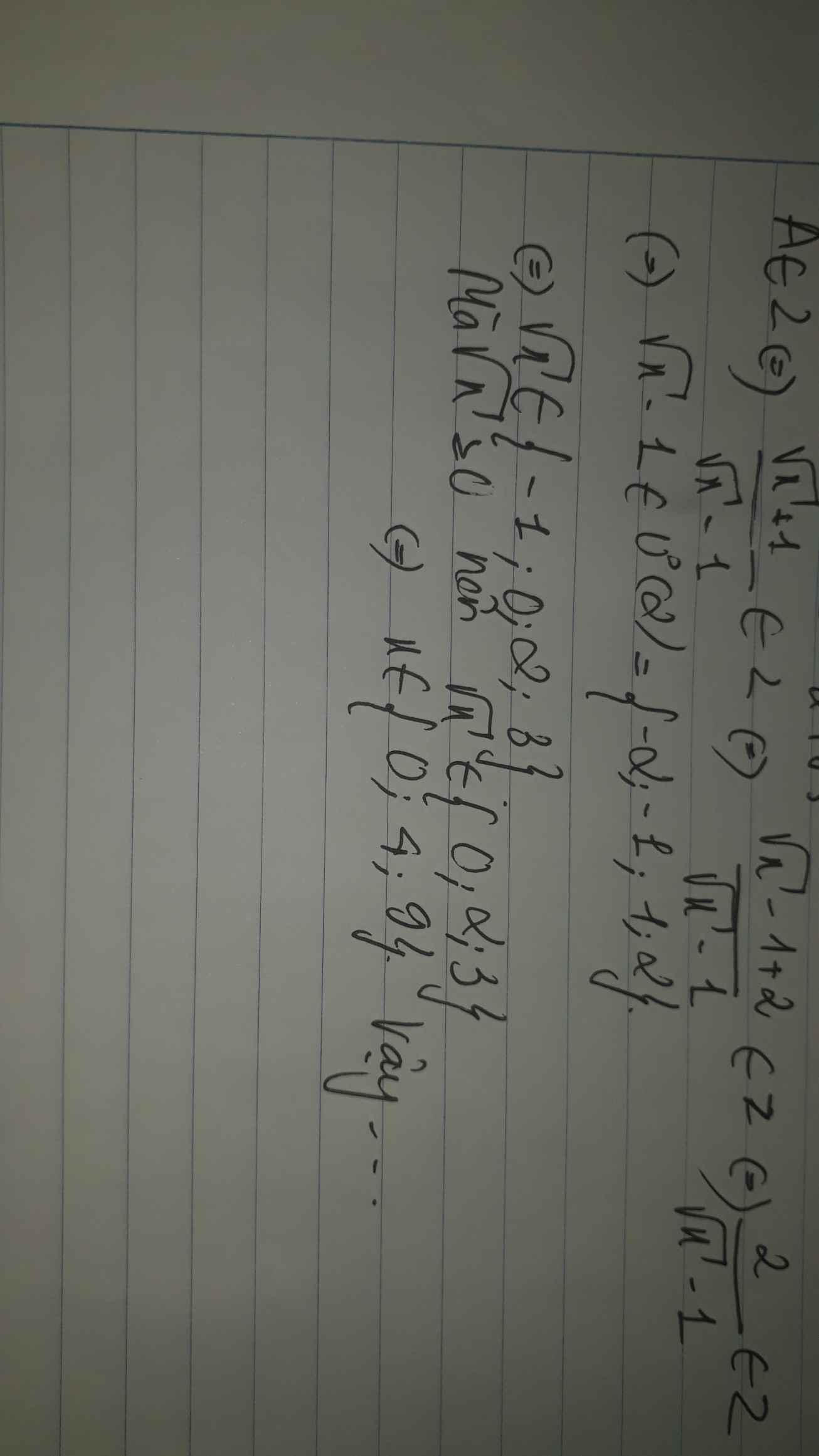


 ai giải giúp em mấy bài toán này vs ạ giải chi tiết giúp em ạ
ai giải giúp em mấy bài toán này vs ạ giải chi tiết giúp em ạ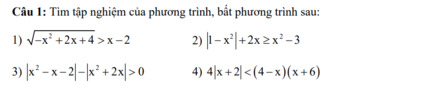
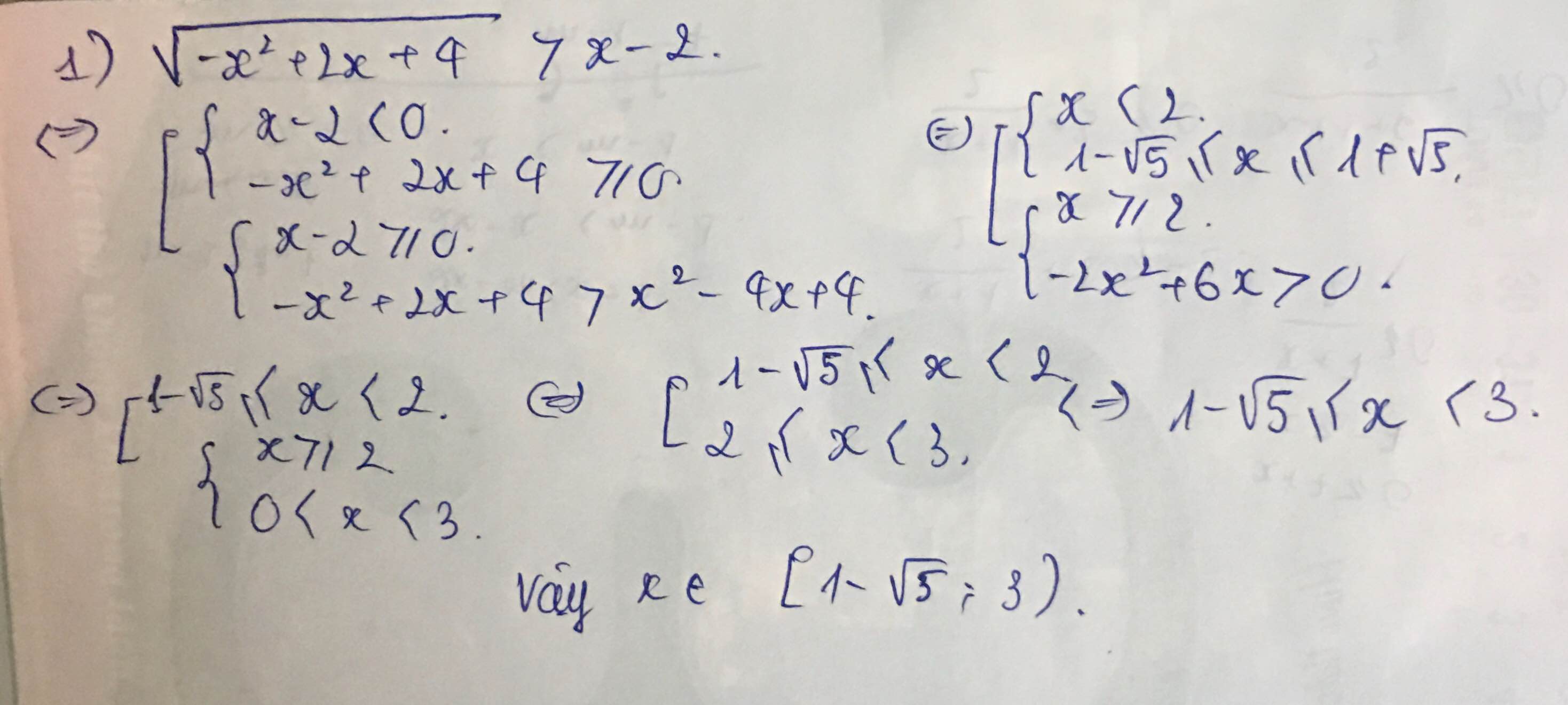
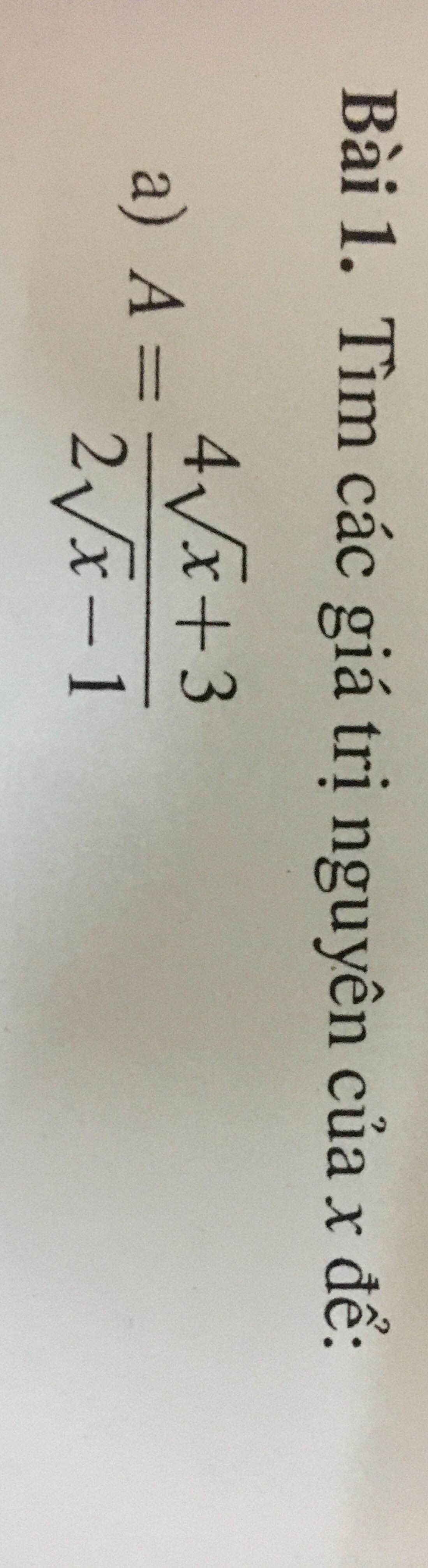


 ai giải giùm em câu 6 vs ạ cho em lời giải chi tiết và vẽ hình giúp em vs ạ cảm ơn mn
ai giải giùm em câu 6 vs ạ cho em lời giải chi tiết và vẽ hình giúp em vs ạ cảm ơn mn
Lời giải:
Dễ thấy $2\sqrt{x}+3>0; 7>0$ nên $A>0$
Mặt khác:
$2\sqrt{x}\geq 0\Rightarrow 2\sqrt{x}+3\geq 3$
$\Rightarrow A=\frac{7}{2\sqrt{x}+3}\leq \frac{7}{3}$
Vậy $0< A< \frac{7}{3}$
$A\in\mathbb{Z}\Leftrightarrow A\in\left\{1;2\right\}$
$\Leftrightarrow \frac{7}{2\sqrt{x}+3}\in \left\{1;2\right\}$
$\Leftrightarrow x\in\left\{4; \frac{1}{16}\right\}$
Để A là số nguyên thì \(7⋮2\sqrt{x}+3\)
\(\Leftrightarrow2\sqrt{x}+3=7\)
\(\Leftrightarrow2\sqrt{x}=4\)
hay x=4