Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
a: MD//AC
=>góc MDB=góc ACB
=>góc MDB=60 độ
Xét tứ giác BEMD có
EM//BD
góc B=góc MDB
=>BEMD là hình thang cân
ME//BC
=>góc AEM=góc ABD=60 độ
Xét tứ giác AEMF có
MF//AE
góc A=góc MEA
=>AEMF là hình thang cân
MF//AE
=>góc CFM=góc CAB=60 độ
Xét tứ giác DCFM có
DM//FC
góc DCF=góc MFC
=>DCFM là hình thang cân
b: Sửa đề: Độ dài 3 cạnh MA,MB,MC bằng độ dài 3 cạnh của tam giác nào
AEMF là hình thang cân
=>AM=EF
BEMD là hình thang cân
=>BM=ED
FMDC là hình thang cân
=>MC=FD
=>Độ dài 3 cạnh MA,MB,MC bằng độ dài 3 cạnh của ΔEFD
bài 1 sai đề rồi bạn. Nếu BEMD là ht cân thật thì \(\widehat{ABC}=\widehat{MDB}\)mà \(\widehat{MDB}=\widehat{ACB}\)(đồng vị) => \(\widehat{ABC}=\widehat{ACB}\)=> tam giác ABC cân( trái với đề bài)
xét hình thang MDEC ta có
=> MD//EC
=>góc ACB =MDB (2 góc đồng vị) (1)
mà ABC = ACB ( tam giác ABC là tam giác đều) (2)
TỪ (1) và (2) => ABC = MDB => hình thang FMBD là hình thang cân
a: ME//AB
=>góc CEM=góc CAB=60 độ
=>góc CEM=góc C
Xét tứ giác MECD có
MD//EC
góc MEC=góc DCE
=>MECD là hình thang cân
=>góc EMD=180-60=120 độ
MF//BC
=>góc AFM=góc ABC=60 độ
Xét tứ giác AFME có
ME//AF
góc MFA=góc EAF
=>AFME là hình thang cân
=>góc FME=180-60=120 độ
MD//AC
=>góc MDB=góc ACB=60 độ
=>góc MDB=góc B
Xét tứ giác BFMD có
FM//BD
góc B=góc MDB
=>BFMD là hình thang cân
=>góc FMD=180-60=120 độ
=>góc FME=góc FMD=góc DME
b: AEMF là hình thang cân
=>AM=EF
BFMD là hình thang cân
=>BM=FD
MECD là hình thang cân
=>MC=ED
=>MA,MB,MC lần lượt là độ dài 3 cạnh của ΔDEF
=>Trong 3 đoạn MA,MB,MC, đoạn lớn nhất nhỏ hơn tổng 2 đoạn còn lại
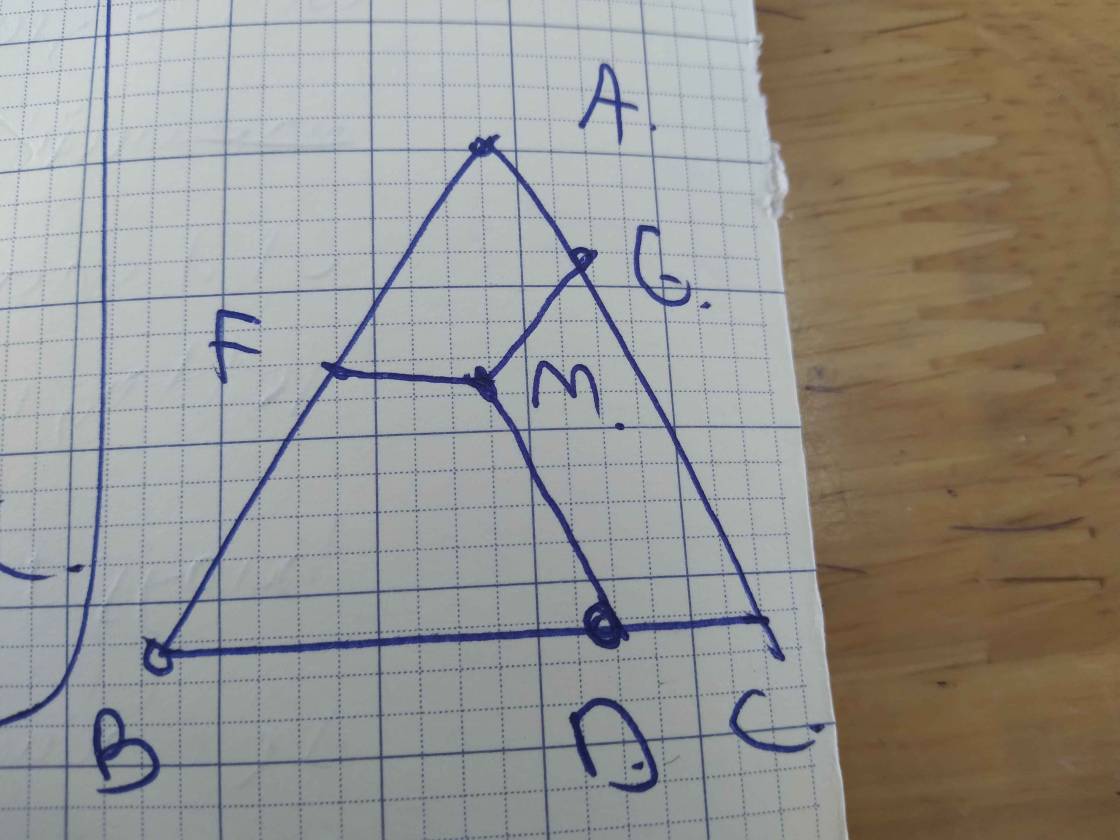
a, Ta có: \(\Delta ABC\) đều \(\Rightarrow\widehat{ABC}=\widehat{ACB}=\widehat{BAC}\)
MD//AC \(\Rightarrow\widehat{BDM}=\widehat{ACB}\) (2 góc đồng vị)
ME//BC \(\Rightarrow\widehat{AEM}=\widehat{ABC}\) (2 góc đồng vị)
MF//AB \(\Rightarrow\widehat{CFM}=\widehat{BAC}\) (2 góc đồng vị)
Do đó: \(\widehat{BDM}=\widehat{ACB}=\widehat{AEM}=\widehat{ABC}=\widehat{CFM}=\widehat{BAC}\)
hay \(\widehat{BDM}=\widehat{DBE}=\widehat{AEM}=\widehat{EAF}=\widehat{CFM}=\widehat{FCD}\)
Vì MD//AC và \(\widehat{CFM}=\widehat{FCD}\) => DMFC là hình thang cân
ME//BC và \(\widehat{BDM}=\widehat{DBE}\) => BEMD là hình thang cân
MF//AB và \(\widehat{AEM}=\widehat{EAF}\) => AFME là hình thang cân
=> đpcm
b, Ta có: hình thang AFME cân => MA=FE
hình thang BEMD cân => MB=ED
hình thang DMFC cân => MC=DF
=> độ dài các đoạn MA, MB, MC lần lượt bằng độ dài các cạnh FE, ED, DF của \(\Delta DEF\)
Vậy...
Cảm ơn bạn nhiều nha! Mk đã giải được rồi :3