Giúp em bài này vs em cảm ơn 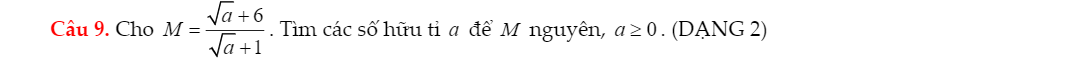
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Tham khảo: Cho tứ giác ABCD có góc C + góc D = 90 độ. Gọi M, N, P, Q theo thứ tự là trung điểm của AB, BD, DC, CA. Chứng minh 4 điểm M, N, P, Q cùng nằm trên 1 đường tròn - Toán học Lớp 9 - Bài tập Toán học Lớp 9 - Giải bài tập Toán học Lớp 9 | Lazi.vn - Cộng đồng Tri thức & Giáo dục


Xét ΔABD có
M là trung điểm của AB
S là trung điểm của AD
Do đó: MS là đường trung bình của ΔBAD
Suy ra: MS//BD và \(MS=\dfrac{BD}{2}\left(1\right)\)
mà BD\(\perp\)AC
nên MS\(\perp\)AC
Xét ΔABC có
M là trung điểm của AB
N là trung điểm của BC
Do đó: MN là đường trung bình của ΔABC
Suy ra: MN//AC
và AC\(\perp\)MS
nên MN\(\perp\)MS
Xét ΔBCD có
N là trung điểm của BC
R là trung điểm của CD
Do đó: RN là đường trung bình của ΔBCD
Suy ra: RN//BD và \(RN=\dfrac{BD}{2}\left(2\right)\)
Từ \(\left(1\right),\left(2\right)\) suy ra MS//NR và MS=NR
Xét tứ giác MSRN có
MS//NR
MS=NR
Do đó: MSRN là hình bình hành
mà \(\widehat{SMN}=90^0\)
nên MSRN là hình chữ nhật
Suy ra: M,S,R,N cùng thuộc 1 đường tròn

1 composer
2 successful
3 powerful
4 inspiration
5 hope
6 nominated
7 patriotism
8 performing
9 influenced
10 singer

\(m_{NaOH}=a\left(g\right),V_{dd_{NaOH}}=b\left(l\right)\)
\(n_{NaOH}=\dfrac{a}{40}\left(mol\right)\)
\(n_{NaOH}=0.5b\left(mol\right)\)
\(n_{NaOH\left(2M\right)}=2.5\cdot2=5\left(mol\right)\)
\(\Rightarrow\dfrac{a}{40}+0.5b=5\left(1\right)\)
\(m_{dd_{NaOH}}=2500\cdot1.06=2650\left(g\right)\)
\(\Rightarrow a+1000b\cdot1.06=2650\left(2\right)\)
\(\left(1\right),\left(2\right):\)
Số lẻ quá em ơi :<
\(\)

Bài 4:
a, Nhóm từ a dùng để tả các mức độ mùi hương của sự vật
b, Nhóm tử b dùng để diễn tả trạng thái thăng hoa, toả sáng của sự vật.

a) \(A=x^4+4x+7=\left(x^2+4x+4\right)+3=\left(x+2\right)^2+3\ge3\)
\(minA=3\Leftrightarrow x=-2\)
b) \(B=x^2-x+1=\left(x^2-x+\dfrac{1}{4}\right)+\dfrac{3}{4}=\left(x-\dfrac{1}{2}\right)^2+\dfrac{3}{4}\ge\dfrac{3}{4}\)
\(minB=\dfrac{3}{4}\Leftrightarrow x=\dfrac{1}{2}\)
c) \(C=4x-x^2+3=-\left(x^2-4x+4\right)+7=-\left(x-2\right)^2+7\le7\)
\(maxC=7\Leftrightarrow x=2\)
d) \(D=2x-2x^2-5=-2\left(x^2-x+\dfrac{1}{4}\right)-\dfrac{9}{2}=-2\left(x-\dfrac{1}{2}\right)^2-\dfrac{9}{2}\le-\dfrac{9}{2}\)
\(maxD=-\dfrac{9}{2}\Leftrightarrow x=\dfrac{1}{2}\)

\(2\left(\overrightarrow{IA}+\overrightarrow{AB}\right)+3\left(\overrightarrow{IA}+\overrightarrow{AC}\right)=\overrightarrow{0}\Leftrightarrow5\overrightarrow{IA}+2\overrightarrow{AB}+3\overrightarrow{AC}=\overrightarrow{0}\)
\(\Leftrightarrow\overrightarrow{AI}=\dfrac{2}{5}\overrightarrow{AB}+\dfrac{3}{5}\overrightarrow{AC}\)
\(\overrightarrow{JB}+\overrightarrow{BA}+3\overrightarrow{JB}+3\overrightarrow{BC}=\overrightarrow{0}\Leftrightarrow\overrightarrow{BJ}=-\dfrac{1}{4}\overrightarrow{AB}+\dfrac{3}{4}\overrightarrow{BC}=-\dfrac{1}{4}\overrightarrow{AB}+\dfrac{3}{4}\overrightarrow{BA}+\dfrac{3}{4}\overrightarrow{AC}\)
\(=-\overrightarrow{AB}+\dfrac{3}{4}\overrightarrow{AC}\)
\(\Rightarrow\overrightarrow{AI}.\overrightarrow{BJ}=\left(\dfrac{2}{5}\overrightarrow{AB}+\dfrac{3}{5}\overrightarrow{AC}\right)\left(-\overrightarrow{AB}+\dfrac{3}{4}\overrightarrow{AC}\right)\)
\(=-\dfrac{2}{5}AB^2+\dfrac{9}{20}AC^2-\dfrac{3}{10}\overrightarrow{AB}.\overrightarrow{AC}\)
\(=-\dfrac{3}{5}a^2+\dfrac{9}{20}a^2-\dfrac{3}{10}a^2.cos60^0=-\dfrac{3}{10}a^2\)
b.
Từ câu a ta có
\(\overrightarrow{AI}=\dfrac{2}{5}\overrightarrow{AB}+\dfrac{3}{5}\overrightarrow{AC}\) (1)
\(\overrightarrow{JA}+3\overrightarrow{JC}=\overrightarrow{0}\Leftrightarrow\overrightarrow{JA}+3\overrightarrow{JA}+3\overrightarrow{AC}=\overrightarrow{0}\Leftrightarrow\overrightarrow{JA}=-\dfrac{3}{4}\overrightarrow{AC}\) (2)
Cộng vế (1) và (2):
\(\overrightarrow{JA}+\overrightarrow{AI}=-\dfrac{3}{4}\overrightarrow{AC}+\dfrac{2}{5}\overrightarrow{AB}+\dfrac{3}{5}\overrightarrow{AC}\)
\(\Leftrightarrow\overrightarrow{JI}=\dfrac{2}{5}\overrightarrow{AB}-\dfrac{3}{20}\overrightarrow{AC}\)
\(\Rightarrow IJ^2=\overrightarrow{JI}^2=\left(\dfrac{3}{5}\overrightarrow{AB}-\dfrac{3}{20}\overrightarrow{AC}\right)^2=\dfrac{9}{25}AB^2+\dfrac{9}{400}AC^2-\dfrac{9}{50}\overrightarrow{AB}.\overrightarrow{AC}\)
\(=\dfrac{9}{25}a^2+\dfrac{9}{400}a^2-\dfrac{9}{50}.a^2.cos60^0=...\)


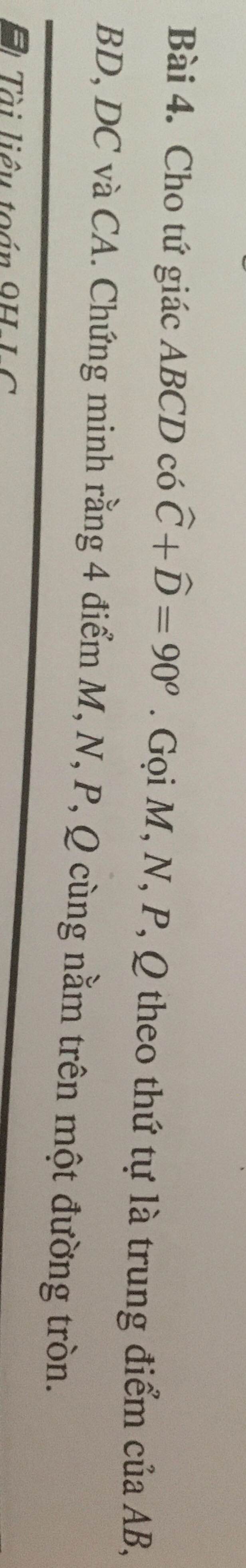




 Giúp em 2 bài này vs ạ, em cảm ơn!
Giúp em 2 bài này vs ạ, em cảm ơn! giúp em bài này vs ạ em cảm ơn trc ạ
giúp em bài này vs ạ em cảm ơn trc ạ





Để M nguyên thì \(5⋮\sqrt{a}+1\)
\(\Leftrightarrow\sqrt{a}+1\in\left\{1;5\right\}\)
\(\Leftrightarrow\sqrt{a}\in\left\{0;4\right\}\)
hay \(a\in\left\{0;16\right\}\)