Tìm GTLN của y=11+\(\sqrt{1-22x-x^2}\)
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

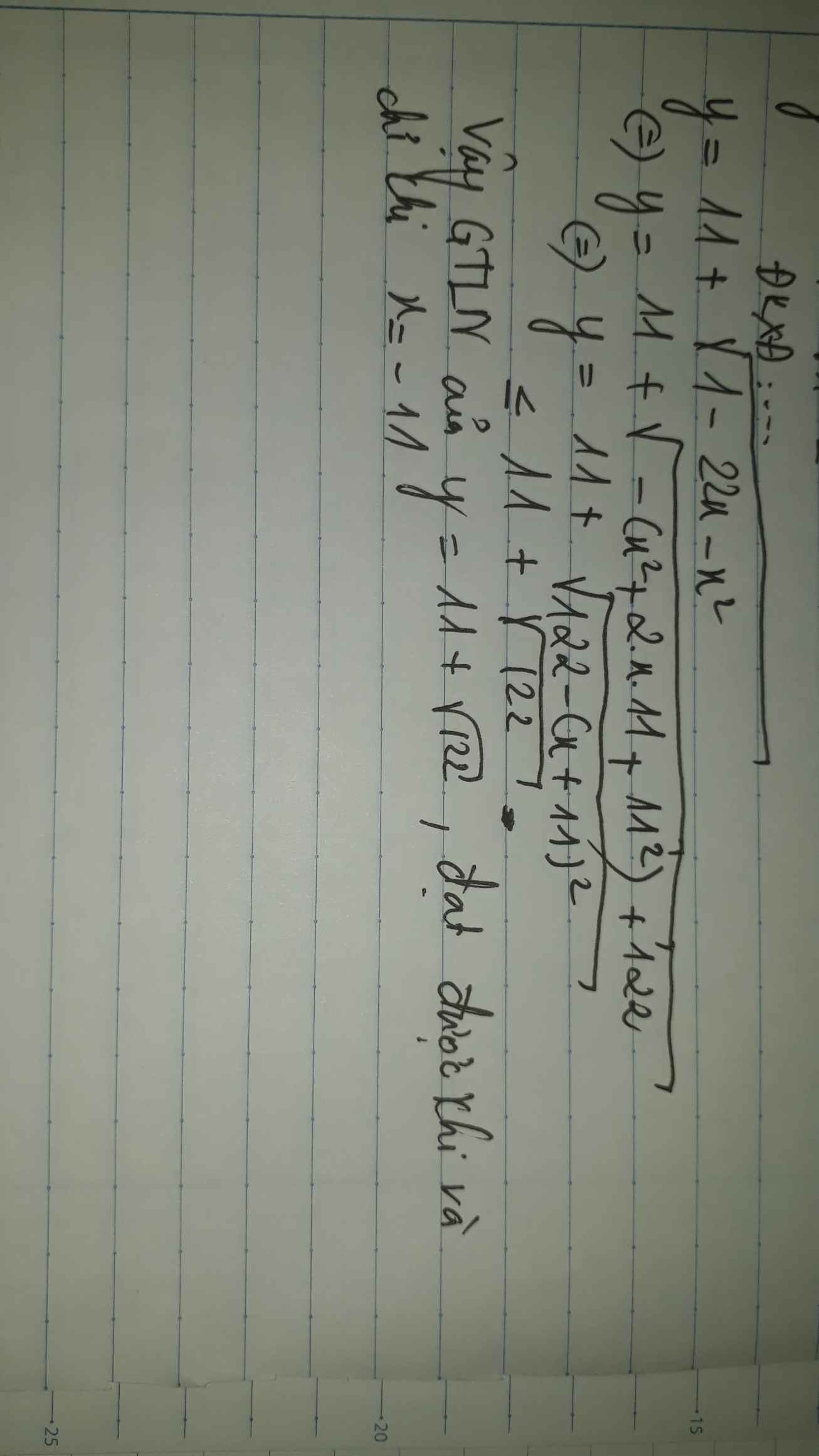

1.
\(y=\sqrt{5-2\cos ^2x\sin ^2x}=\sqrt{5-\frac{1}{2}(2\cos x\sin x)^2}=\sqrt{5-\frac{1}{2}\sin ^22x}\)
Dễ thấy:
$\sin ^22x\geq 0\Rightarrow y=\sqrt{5-\frac{1}{2}\sin ^22x}\leq \sqrt{5}$
Vậy $y_{\max}=\sqrt{5}$
$\sin ^22x\leq 1\Rightarrow y=\sqrt{5-\frac{1}{2}\sin ^22x}\geq \sqrt{5-\frac{1}{2}}=\frac{3\sqrt{2}}{2}$
Vậy $y_{\min}=\frac{3\sqrt{2}}{2}$
2.
$y=1+\frac{1}{2}\sin 2x\cos 2x=1+\frac{1}{4}.2\sin 2x\cos 2x$
$=1+\frac{1}{4}\sin 4x$
Vì $-1\leq \sin 4x\leq 1$
$\Rightarrow \frac{5}{4}\leq 1+\frac{1}{4}\sin 4x\leq \frac{3}{4}$
$\Leftrightarrow \frac{5}{4}\leq y\leq \frac{3}{4}$
Vậy $y_{\max}=\frac{5}{4}; y_{\min}=\frac{3}{4}$

1: \(y=x+\dfrac{4}{\left(x-2\right)^2}\)
\(\Leftrightarrow y'=1+\left(\dfrac{4}{\left(x-2\right)^2}\right)'\)
=>\(y'=1+\dfrac{4'\left(x-2\right)^2-4\left[\left(x-2\right)^2\right]'}{\left(x-2\right)^4}\)
=>\(y'=1+\dfrac{-4\cdot2\cdot\left(x-2\right)'\left(x-2\right)}{\left(x-2\right)^4}\)
=>\(y'=1-\dfrac{8}{\left(x-2\right)^3}\)
Đặt y'=0
=>\(\dfrac{8}{\left(x-2\right)^3}=1\)
=>\(\left(x-2\right)^3=8\)
=>x-2=2
=>x=4
Đặt \(f\left(x\right)=x+\dfrac{4}{\left(x-2\right)^2}\)
\(f\left(4\right)=4+\dfrac{4}{\left(4-2\right)^2}=4+1=5\)
\(f\left(0\right)=0+\dfrac{4}{\left(0-2\right)^2}=0+\dfrac{4}{4}=1\)
\(f\left(5\right)=5+\dfrac{4}{\left(5-2\right)^2}=5+\dfrac{4}{9}=\dfrac{49}{9}\)
Vì f(0)<f(4)<f(5)
nên \(f\left(x\right)_{max\left[0;5\right]\backslash\left\{2\right\}}=f\left(5\right)=\dfrac{49}{9}\) và \(f\left(x\right)_{min\left[0;5\right]\backslash\left\{2\right\}}=1\)
2: \(y=cos^22x-sinx\cdot cosx+4\)
\(=1-sin^22x-\dfrac{1}{2}\cdot sin2x+4\)
\(=-sin^22x-\dfrac{1}{2}\cdot sin2x+5\)
\(=-\left(sin^22x+\dfrac{1}{2}\cdot sin2x-5\right)\)
\(=-\left(sin^22x+2\cdot sin2x\cdot\dfrac{1}{4}+\dfrac{1}{16}-\dfrac{81}{16}\right)\)
\(=-\left(sin2x+\dfrac{1}{4}\right)^2+\dfrac{81}{16}\)
\(-1< =sin2x< =1\)
=>\(-\dfrac{3}{4}< =sin2x+\dfrac{1}{4}< =\dfrac{5}{4}\)
=>\(0< =\left(sin2x+\dfrac{1}{4}\right)^2< =\dfrac{25}{16}\)
=>\(0>=-\left(sin2x+\dfrac{1}{4}\right)^2>=-\dfrac{25}{16}\)
=>\(\dfrac{81}{16}>=-sin\left(2x+\dfrac{1}{4}\right)^2+\dfrac{81}{16}>=-\dfrac{25}{16}+\dfrac{81}{16}=\dfrac{7}{2}\)
=>\(\dfrac{81}{16}>=y>=\dfrac{7}{2}\)
\(y_{min}=\dfrac{7}{2}\) khi \(sin2x+\dfrac{1}{4}=\dfrac{5}{4}\)
=>\(sin2x=1\)
=>\(2x=\dfrac{\Omega}{2}+k2\Omega\)
=>\(x=\dfrac{\Omega}{4}+k\Omega\)
\(y_{max}=\dfrac{81}{16}\) khi sin 2x=-1
=>\(2x=-\dfrac{\Omega}{2}+k2\Omega\)
=>\(x=-\dfrac{\Omega}{4}+k\Omega\)

a, Hàm số xác định khi: \(\left\{{}\begin{matrix}cos\dfrac{x}{2}\ne3\\tanx\ne\sqrt{3}\\cosx\ne0\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x\ne\dfrac{\pi}{3}+k\pi\\x\ne\dfrac{\pi}{2}+k\pi\end{matrix}\right.\)

a) Rút gọn P
ĐKXĐ: \(x\ge0;x\ne1\)
\(P=\dfrac{15\sqrt{x}-11}{x+2\sqrt{x}-3}-\dfrac{3\sqrt{x}-2}{\sqrt{x}-1}-\dfrac{2\sqrt{x}+3}{\sqrt{x}+3}\)
\(=\dfrac{15\sqrt{x}-11}{\left(\sqrt{x}-1\right)\left(\sqrt{x}+3\right)}\)\(-\dfrac{\left(3\sqrt{x}-2\right)\left(\sqrt{x}+3\right)}{\left(\sqrt{x}-1\right)\left(\sqrt{x}+3\right)}\)\(-\dfrac{\left(2\sqrt{x}+3\right)\left(\sqrt{x}-1\right)}{\left(\sqrt{x}+3\right)\left(\sqrt{x}-1\right)}\)
\(=\dfrac{15\sqrt{x}-11-\left(3x+9\sqrt{x}-2\sqrt{x}-6\right)-\left(2x-2\sqrt{x}+3\sqrt{x}-3\right)}{\left(\sqrt{x}+3\right)\left(\sqrt{x}-1\right)}\)
\(=\dfrac{15\sqrt{x}-11-3x-7\sqrt{x}+6-2x-\sqrt{x}+3}{\left(\sqrt{x}+3\right)\left(\sqrt{x}-1\right)}\)
\(=\dfrac{-5x+7\sqrt{x}-2}{\left(\sqrt{x}+3\right)\left(\sqrt{x}-1\right)}\)\(=\dfrac{\left(-5\sqrt{x}+2\right)\left(\sqrt{x}-1\right)}{\left(\sqrt{x}+3\right)\left(\sqrt{x}-1\right)}\)
\(=\dfrac{-5\sqrt{x}+2}{\sqrt{x}+3}\)\(=\dfrac{2-5\sqrt{x}}{\sqrt{x}+3}\)
b) Tìm GTLN
\(P=\dfrac{2-5\sqrt{x}}{\sqrt{x}+3}=\dfrac{17-5\left(\sqrt{x}+3\right)}{\sqrt{x}+3}=\dfrac{17}{\sqrt{x}+3}-5\)
Ta có: \(\sqrt{x}\ge0\Rightarrow\sqrt{x}+3\ge3\Rightarrow P=\dfrac{17}{\sqrt{x}+3}-5\le\dfrac{17}{3}-5=\dfrac{2}{3}\)
Dấu "=" xảy ra khi \(x=0\)
Vậy \(P_{max}=\dfrac{2}{3}\) khi \(x=0\)

1:
\(A=\dfrac{15\sqrt{x}-11-\left(3\sqrt{x}-2\right)\left(\sqrt{x}+3\right)-\left(2\sqrt{x}+3\right)\left(\sqrt{x}-1\right)}{\left(\sqrt{x}+3\right)\left(\sqrt{x}-1\right)}\)
\(=\dfrac{15\sqrt{x}-11-3x-9\sqrt{x}+2\sqrt{x}+6-2x+2\sqrt{x}-3\sqrt{x}+3}{\left(\sqrt{x}+3\right)\left(\sqrt{x}-1\right)}\)
\(=\dfrac{-5x+7\sqrt{x}-2}{\left(\sqrt{x}+3\right)\left(\sqrt{x}-1\right)}=\dfrac{-5\sqrt{x}+2}{\sqrt{x}+3}\)
3: A nguyên
=>-5căn x-15+17 chia hết cho căn x+3
=>căn x+3 thuộc Ư(17)
=>căn x+3=17
=>x=196

Bài 2:Áp dụng BĐT AM-GM ta có:
\(\frac{1}{x}+\frac{1}{y}\ge2\sqrt{\frac{1}{xy}}\)
\(\frac{1}{y}+\frac{1}{z}\ge2\sqrt{\frac{1}{yz}}\)
\(\frac{1}{x}+\frac{1}{z}\ge2\sqrt{\frac{1}{xz}}\)
CỘng theo vế 3 BĐT trên có:
\(2\left(\frac{1}{x}+\frac{1}{y}+\frac{1}{z}\right)\ge2\left(\frac{1}{\sqrt{xy}}+\frac{1}{\sqrt{yz}}+\frac{1}{\sqrt{xz}}\right)\)
Khi x=y=z
Ta có: \(\frac{1}{\sqrt{1}}>\frac{1}{\sqrt{100}}\)
\(\frac{1}{\sqrt{2}}>\frac{1}{\sqrt{100}}\)
\(\frac{1}{\sqrt{3}}>\frac{1}{\sqrt{100}}\)
\(..........................\)
\(\frac{1}{\sqrt{99}}>\frac{1}{\sqrt{100}}\)
\(\frac{1}{\sqrt{100}}=\frac{1}{\sqrt{100}}\)
Cộng theo vế ta có:
\(\frac{1}{\sqrt{1}}+\frac{1}{\sqrt{2}}+...+\frac{1}{\sqrt{100}}>\frac{1}{10}+\frac{1}{10}+...+\frac{1}{10}=\frac{100}{10}=10\)

Lời giải:
TXĐ: $[-1;1]$
$y'=\frac{1}{2\sqrt{x+1}}-\frac{1}{2\sqrt{1-x}}+\frac{x}{2}$
$y'=0\Leftrightarrow x=0$
$f(0)=2$;
$f(1)=f(-1)=\sqrt{2}+\frac{1}{4}$
Vậy $f_{\min}=2; f_{\max}=\frac{1}{4}+\sqrt{2}$

y=(sin2x-3)^2-6
-1<=sin2x<=1
=>-4<=sin2x-3<=-2
=>4<=(sin2x-3)^2<=16
=>-2<=y<=10
y min khi sin2x-3=-2
=>sin 2x=1
=>2x=pi/2+k2pi
=>x=pi/4+kpi
y max khi sin 2x-3=-4
=>sin 2x=-1
=>2x=-pi/2+k2pi
=>x=-pi/4+kpi

\(\sqrt{4x+2\sqrt{x}+1}\le\sqrt{4x+\dfrac{1}{2}\left(2^2+x\right)+1}=\sqrt{\dfrac{9x}{2}+3}\)
\(=\dfrac{1}{\sqrt{21}}.\sqrt{21}.\sqrt{\dfrac{9x}{2}+3}\le\dfrac{1}{2\sqrt{21}}\left(21+\dfrac{9x}{2}+3\right)=\dfrac{1}{2\sqrt{21}}\left(\dfrac{9x}{2}+24\right)\)
Tương tự và cộng lại:
\(A\le\dfrac{1}{2\sqrt{21}}\left(\dfrac{9}{2}\left(x+y+z\right)+72\right)=3\sqrt{21}\)
\(A_{max}=3\sqrt{21}\) khi \(x=y=z=4\)
\(A=1\sqrt{4x+2\sqrt{x}+1}+1.\sqrt{4y+2\sqrt{y}+1}+1\sqrt{4z+2\sqrt{z}+1}\)
\(\le\sqrt{\left(1+1+1\right)\left(4\left(x+y+z\right)+2\left(\sqrt{x}+\sqrt{y}+\sqrt{z}\right)+3\right)}\)
\(=\sqrt{3.\left[51+\dfrac{4\left(\sqrt{x}+\sqrt{y}+\sqrt{z}\right)}{2}\right]}\)
\(\le\sqrt{3.\left[51+\dfrac{x+y+z+12}{2}\right]}\)
\(=\sqrt{189}\)
Dấu "=" xảy ra <=> x = y = z = 4
