Cho 3 tia Ox, Oy , Oz sao cho xOy=zOy=xOz. Gọi Ox' , Oy' , Oz' lần lượt là tia đối của các tia Ox , Oy , Oz .
a,CMR : Tia Ox' , Oy' , Oz' lần lượt là tia phân giác cho xOy,zOy,xOz.
b, Tính số đo cua các góc xOy,zOy,xOz.
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

O x z y y'
a)Trên cùng 1nmp có bờ chứa tia Ox, có gxOy>gxOz(100*>30*)
Nên Oz nằm giữa 2 tia Ox, Oy
mà Oy' là tia đối của tia Oy
nên Ox nằm giữa 2 tia Oz,Oy'
câu a hình như đề sai, 1 là :Ox nằm giữa 2 tia Oz;Oy' hoặc Ox nằm giữa 2 tia Oy, Oy'
2 là: Oz nằm giữa 2 tia Ox,Oy
đó nha, a đề sai

a) Vì \(\widehat{xOz}=75^o\)
\(\widehat{xOy}=150^o\)
Mà \(xOz+zOy=xOy\)
=> Oz là tia nằm giữa hai tia Ox và Oy
b) Vì
\(xOz+zOy=xOy\)
Mà \(xOz=75^o\)
\(xOy=150^o\)
\(\Rightarrow75^o+zOy=150^o\)
\(\Rightarrow zOy=150-75\)
\(\Rightarrow zOy=85^o\)
+) Vì \(xOz=75^o\left(GT\right)\)[ Đề bài cho ] (1)
ta có : \(zOy=85^o\)( tính ở trên ) (2)
Từ (1) ;(2)
Vậy \(xOz< zOy\left(75^o< 85^o\right)\)
c) Ta có :
\(xOz+zOy=xOy\)
Muốn có phân giác thì 2 góc phải bằng nhau
mà \(xOz< zOy\)( chứng minh trên )
=> Oz không là phân giác của góc xOy .

O x z y y'
Tự đánh góc
Vì xOy < xOz (35 < 70)
=> Tia Oy nằm giữa 2 tia Oz và Ox
=> xOy + yOz = xOz
=> yOz = 35o
Có : yOz = xOy = 35o
Tia Oy nằm giữa 2 tia Oz và Ox
=> Oy là p/g xOz
c) Oy' là tia đối Oy
=> zOy' và zOy kề bù
=> zOy' + zOy = 180o
=> zOy' = 145o
Oy' là tia đối Oy
=> xOy và xOy' kề bù
=> xOy + xOy' = 180o
=> xOy' = 145o
Rồi tự so sánh đi

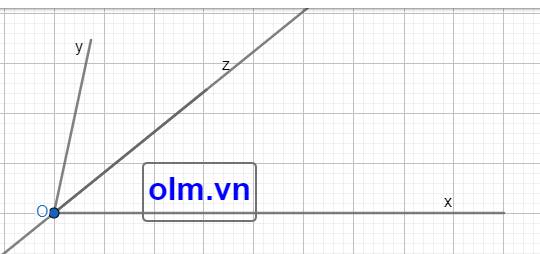
a, Trên cùng một nửa mặt phẳng có bờ là tia ox vì \(\widehat{xOy}\) > \(\widehat{xOz}\) nên Oz nằm giữa hai tia Oy và Ox.
b, \(\widehat{xOy}\) = \(\widehat{xOz}\) + \(\widehat{zOy}\) ⇒ \(\widehat{zOy}\) = 800 - 400 = 400
c, Oz nằm giữa hai tia Oy và Ox và \(\widehat{zOy}\) = \(\widehat{xOz}\) nên OZ là tia phân giác của góc xOy

a) Trên cùng một nửa mặt phẳng bờ chứa tia Ox, ta có: \(\widehat{xOz}< \widehat{xOy}\left(45^0< 135^0\right)\)
nên tia Oz nằm giữa hai tia Ox và Oy
b) Ta có: tia Oz nằm giữa hai tia Ox và Oy(cmt)
nên \(\widehat{xOz}+\widehat{yOz}=\widehat{xOy}\)
\(\Leftrightarrow\widehat{yOz}+45^0=135^0\)
hay \(\widehat{yOz}=90^0\)