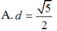Cho hình thoi ABCD có cạnh bằng a và 2 đường chéo cắt nhau tại H. Gọi đường tròn tâm O bán kính r đi qua 3 đỉnh của tam giác ABC. Gọi đường tròn tâm O' bán kính R đi qua 3 đỉnh của tam giác ABC.
CM: a) \(\dfrac{AH}{BH}\)= \(\dfrac{r}{R}\)
b) \(\dfrac{1}{R^2}\)+\(\dfrac{1}{r^2}=\dfrac{4}{a^2}\)
c)Tính diện tích hình thoi ABCD theo R.
Mình cần gấp trước trưa mai mọi người giúp dùm với![]()
![]()
![]()
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Lời giải:
a)
$\widehat{ABD}=\widehat{DCA}=90^0$ (góc nt chắn nửa đường tròn)
$\Leftrightarrow \widehat{ABE}=\widehat{DCE}=90^0$
Tứ giác $ABEH$ có tổng 2 góc đối $\widehat{ABE}+\widehat{AHE}=90^0+90^0=180^0$ nên là tứ giác nội tiếp.
Tứ giác $DCEH$ có tổng 2 góc đối $\widehat{DCE}+\widehat{EHD}=90^0+90^0=180^0$ nên là tứ giác nội tiếp.
b)
Từ 2 tứ giác nội tiếp phần a, kết hợp với $ABCD$ là tứ giác nội tiếp, ta có:
\(\widehat{HBE}=\widehat{EAH}=\widehat{CAD}=\widehat{CBD}=\widehat{CBE}\) nên $BE$ là tia phân giác $\widehat{HBC}$
\(\widehat{HCE}=\widehat{EDH}=\widehat{BDA}=\widehat{BCA}=\widehat{BCE}\) nên $CE$ là tia phân giác $\widehat{BCH}$
Do đó $E$ chính là tâm đường tròn nội tiếp tam giác $BCH$
c) Sử dụng tính chất trung tuyến ứng với cạnh huyền thì bằng nửa cạnh huyền. Suy ra $IH=IC=EI=ID$.
Ta có:
\(\widehat{IHD}=\widehat{IDH}=\widehat{ODB}=\widehat{OBD}=\widehat{OBI}\) nên $OBIH$ là tứ giác nội tiếp $(1)$
Mặt khác:
$\widehat{HIC}=\widehat{HIB}+\widehat{CIB}$
$=2\widehat{IDH}+2\widehat{CDI}$
$=2\widehat{HDC}=2\widehat{ADC}=2(90^0-\widehat{CAD})$
$=180^0-2\widehat{CBE}=180^0-\widehat{CBH}$
$\Rightarrow BHIC$ là tứ giác nội tiếp $(2)$
Từ $(1);(2)$ suy ra đpcm.

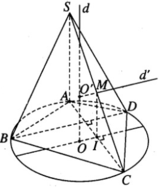
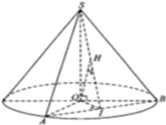
Trong mặt phẳng chứa đường tròn tâm O ngoại tiếp tứ giác ABCD ta kẻ đường kính qua O vuông góc với dây cung AC tại I. Ta có IA = IC và OI // BD. Gọi O’ là tâm mặt cầu đi qua 5 đỉnh của hình chóp. Khi đó điểm O’ phải nằm trên trục d của đường tròn ngoại tiếp tứ giác ABCD. Ta có d ⊥ (ABCD) tại O. Gọi M là trung điểm của cạnh SC. Ta có MI // SA nên MI ⊥ (ABCD) tại I. Từ M kẻ đường thẳng d’ // OI cắt d tại O’. Vì d′ ⊥ (SAC) tại M nên ta có O’C = O’S và O’C là bán kính r của mặt cầu ngoại tiếp hình chóp S.ABCD
Ta có:
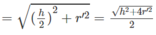

1) Xét (O) có
ΔDAB nội tiếp đường tròn (O)(Vì D,A,B∈(O))
mà AB là đường kính của (O)(gt)
nên ΔDAB vuông tại D(Định lí)
⇒BD⊥AD tại D
hay BD⊥AC
Xét (O) có
ΔEAB nội tiếp đường tròn(E,A,B∈(O))
mà AB là đường kính(gt)
nên ΔEAB vuông tại E(Định lí)
⇒AE⊥EB tại E
hay AE⊥BC tại E
Xét ΔCAB có
BD là đường cao ứng với cạnh AC(cmt)
AE là đường cao ứng với cạnh BC(cmt)
BD\(\cap\)AE={H}
Do đó: H là trực tâm của ΔCAB(Tính chất ba đường cao của tam giác)
⇔CH là đường cao ứng với cạnh AB
hay CH⊥AB(đpcm)

a)Nối F với D : E với D ta có:
Xét tam giác FBC ta có
D là trung điểm BC(1)
Góc BFC=90 (2)
Từ (1)(2)=>FD là trung tuyến của tam giác FBC
=>BD=CD=DF(*)
Chứng minh tương tự tam giác EBC
=>DE=DC=DB(**)
Từ (*)(**)=>BD=CD=DF=DE=(1/2BC)
=>B;F;E;C thuộc đừng tròn
=>D là tâm của đường tròn
B) Do B;H;E nằm trên cùng 1 đừng thẳng => H ko thuộc đừng tròn
=>B;H;E;c ko thuộc đừng tròn