Tìm x
(x - 1)3- 2(x+1)2=(2x + 1)(1 - 3x) - 2x(1-x)
Mk cần gấp lắm,2h là mk phải đi học rồi
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
NL
Nguyễn Lê Phước Thịnh
24 tháng 5 2022
Đúng(0)
Những câu hỏi liên quan
10 tháng 8 2017
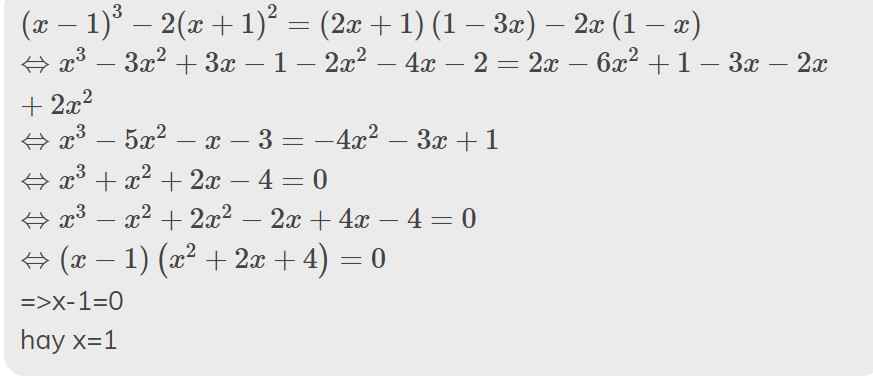
3-4*[(x-1)+(x+1)]=2x+1*1-3x-2x+1+x
-1x=2x-3x-2x+1+x
-1x=-3x+1+x
x+x-x=-3+1+1
x=-1
Mk làm luôn ko ghi đề bài
Mk ko chắc chắn lắm
24 tháng 5 2022
\(\left(x-1\right)^3-2\left(x+1\right)^2=\left(2x+1\right)\left(1-3x\right)-2x\left(1-x\right)\)
\(\Leftrightarrow x^3-3x^2+3x-1-2x^2-4x-2=2x-6x^2+1-3x-2x+2x^2\)
\(\Leftrightarrow x^3-5x^2-x-3=-4x^2-3x+1\)
\(\Leftrightarrow x^3+x^2+2x-4=0\)
\(\Leftrightarrow x^3-x^2+2x^2-2x+4x-4=0\)
\(\Leftrightarrow\left(x-1\right)\left(x^2+2x+4\right)=0\)
=>x-1=0
hay x=1
TN
24 tháng 4 2016
a)để -3/x-1 thuộc Z
=>-3 chia hết x-1
=>x-1\(\in\){1,-1,3,-3}
=>x\(\in\){2,0,4,-2}
b)để -4/2x-1 thuộc Z
=>4 chia hết 2x-1
=>2x-1\(\in\){1,-1,2,-2,4,-4}
=>x\(\in\){1;-3;3;-5;7;-9}
c)\(\frac{3x+7}{x-1}=\frac{3\left(x-1\right)+10}{x-1}=\frac{3\left(x-1\right)}{x-1}+\frac{10}{x-1}\in Z\)
=>10 chia hết x-1
=>x-1\(\in\)Ư(10)
bạn tự làm tiếp nhé
22 tháng 2 2022
Bài 1:
a: f(0)=1
f(2)=-3x2+1=-6+1=-5
f(-2)=-3x2+1=-5
f(-1/2)=-3x1/2+1=-3/2+1=-1/2
b: f(x)=-3
=>-3|x|+1=-3
=>-3|x|=-4
=>|x|=4/3
=>x=4/3 hoặc x=-4/3
S
4 tháng 7 2018
1/
a, (x-3)2+(4+x)(4-x)=10
<=>x2-6x+9+(16-x2)=10
<=>-6x+25=10
<=>-6x=-15
<=>x=5/2
còn lại tương tự a
2/
a, \(a^2\left(a+1\right)+2a\left(a+1\right)=\left(a^2+2a\right)\left(a+1\right)=a\left(a+1\right)\left(a+2\right)\)
Vì a(a+1)(a+2) là tích 3 nguyên liên tiếp nên a(a+1)(a+2) chia hết cho 2,3
Mà (2,3)=1
=>a(a+1)(a+2) chia hết cho 6 (đpcm)
b, \(x^2+2x+2=\left(x^2+2x+1\right)+1=\left(x+1\right)^2+1\)
Vì \(\left(x+1\right)^2\ge0\Rightarrow\left(x+1\right)^2+1\ge1>0\left(đpcm\right)\)
c, \(x^2-x+1=\left(x^2-x+\frac{1}{4}\right)+\frac{3}{4}=\left(x-\frac{1}{2}\right)^2+\frac{3}{4}\)
Vì \(\left(x-\frac{1}{2}\right)^2\ge0\Rightarrow\left(x-\frac{1}{2}\right)^2+\frac{3}{4}\ge\frac{3}{4}>0\)(đpcm)
d, \(-x^2+4x-5=-\left(x^2-4x+4\right)-1=-\left(x-2\right)^2-1\)
Vì \(-\left(x-2\right)^2\le0\Rightarrow-\left(x-2\right)^2-1\le-1< 0\) (đpcm)
5 tháng 7 2018
g,\(-4\left(x-1\right)^2+\left(2x+1\right)\left(2x-1\right)=-3\)
\(\Leftrightarrow-4\left(x^2-2x+1\right)+4x^2-1=-3\)
\(\Leftrightarrow-4x^2+8x-4+4x^2-1=-3\)
\(\Leftrightarrow8x=2\)
\(\Leftrightarrow x=\frac{1}{4}\)
bn xem lại đi nha
18 tháng 9 2021
a) \(2x^2-2x-x^2+6=0\)
\(\Leftrightarrow x^2-2x+1+5=0\)
\(\Leftrightarrow\left(x-1\right)^2=-5\) ( vô lý)
Vậy không có x thoả mãn \(2x.\left(x-1\right)-x^2+6=0\)
b) \(x^4-2x^2.\left(3+2x^2\right)+3x^2.\left(x^2+1\right)=-3\)
\(\Leftrightarrow x^4-6x^2-4x^4+3x^4+3x^2+3=0\)
\(\Leftrightarrow3-3x^2=0\)
\(\Leftrightarrow3x^2=3\Leftrightarrow x^2=1\) \(\Leftrightarrow x\in\left\{-1;1\right\}\)
Vậy \(x\in\left\{-1;1\right\}\)
c) \(\left(x+1\right).\left(x^2-x+1\right)-2x=x.\left(x-2\right).\left(x+2\right)\)
\(\Leftrightarrow x^3+1-2x-x.\left(x^2-4\right)=0\)
\(\Leftrightarrow x^3+1-2x-x^3+4x=0\)
\(\Leftrightarrow1+2x=0\Leftrightarrow x=\dfrac{-1}{2}\)
Vậy x=\(\dfrac{-1}{2}\)
d) \(\left(x+3\right).\left(x^2-3x+9\right)-x.\left(x-2\right).\left(x+2\right)=15\)
\(\Leftrightarrow x^3+27-x.\left(x^2-4\right)-15=0\)
\(\Leftrightarrow x^3-27-x^3+4x-15=0\)
\(\Leftrightarrow4x-42=0\)
\(\Leftrightarrow x=10,5\)
Vậy x=10,5
AH
4 tháng 12 2018
10 + (2x - 1) 2 : 3 = 13
=> (2x - 1) 2 : 3 = 13 - 10
=> (2x - 1) 2 : 3 = 3
=> (2x - 1) 2 = 3 . 3
=> (2x - 1) 2 = 3 2
=> 2x - 1 = 3
=> 2x = 3 + 1
=> 2x = 4
=> x = 2
4 tháng 12 2018
10 + (2x - 1)2 : 3 = 13
=> (2x - 1)2 : 3 = 13 - 10
=> (2x - 1 )2 : 3 = 3
=> (2x - 1)2 = 9
=> (2x - 1)2 = 32
=> 2x - 1 = 3
=> 2x = 4
=> x = 2
Vậy x = 2
16 tháng 3 2020
1) Ta có: \(4x^2-1=\left(2x+1\right).\left(3x-5\right)\)
\(\Leftrightarrow\left(2x+1\right).\left(2x-1\right)-\left(2x+1\right).\left(3x-5\right)=0\)
\(\Leftrightarrow\left(2x+1\right).\left[\left(2x-1\right)-\left(3x-5\right)\right]=0\)
\(\Leftrightarrow\left(2x+1\right).\left(2x-1-3x+5\right)=0\)
\(\Leftrightarrow\left(2x+1\right).\left(4-x\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}2x+1=0\\4-x=0\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}2x=-1\\-x=-4\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=-\frac{1}{2}\left(TM\right)\\x=4\left(TM\right)\end{matrix}\right.\)
Vậy \(x=-\frac{1}{2}\) hoặc \(x=4\)
2) Ta có: \(\left(x+1\right)^2=4.\left(x^2-2x+1\right)\)
\(\Leftrightarrow\left(x+1\right)^2-\left[2.\left(x-1\right)\right]^2=0\)
\(\Leftrightarrow\left[\left(x+1\right)+2.\left(x-1\right)\right].\left[\left(x+1\right)-2.\left(x-1\right)\right]=0\)
\(\Leftrightarrow\left(x+1+2x-2\right).\left(x+1-2x+2\right)=0\)
\(\Leftrightarrow\left(3x-1\right).\left(3-x\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}3x-1=0\\3-x=0\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}3x=1\\-x=-3\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=\frac{1}{3}\left(TM\right)\\x=3\left(TM\right)\end{matrix}\right.\)
Vậy \(x=\frac{1}{3}\) hoặc \(x=3\)
3) Ta có: \(2x^3+5x^2-3x=0\)
\(\Leftrightarrow x.\left(2x^2+5x-3\right)=0\)
\(\Leftrightarrow x.\left(2x^2-x+6x-3\right)=0\)
\(\Leftrightarrow x.\left[x.\left(2x-1\right)+3.\left(2x-1\right)\right]=0\)
\(\Leftrightarrow x.\left(x+3\right).\left(2x-1\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}x=0\\x+3=0\\2x+1=0\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=0\\x=-3\\2x=-1\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=0\left(TM\right)\\x=-3\left(TM\right)\\x=-\frac{1}{2}\left(TM\right)\end{matrix}\right.\)
Vậy \(x=0\) hoặc \(x=-3\) hoặc \(x=-\frac{1}{2}\)
4) Ta có: \(2x=3x-2\)
\(\Leftrightarrow2x-3x=-2\)
\(\Leftrightarrow-x=-2\)
\(\Leftrightarrow x=2\left(TM\right)\)
Vậy \(x=2\)
5) Ta có: \(x+15=3x-1\)
\(\Leftrightarrow x-3x=-1-15\)
\(\Leftrightarrow-2x=-16\)
\(\Leftrightarrow x=8\left(TM\right)\)
Vậy \(x=8\)
6) Ta có: \(2-x=0,5x-4\)
\(\Leftrightarrow-x-0,5x=-4-2\)
\(\Leftrightarrow-1,5x=-6\)
\(\Leftrightarrow x=4\left(TM\right)\)
Vậy \(x=4\)
16 tháng 3 2020
1) 4x2-1=(2x+1)(3x-5)
<=> (2x-1)(2x+1)-(2x+1)(3x-5)=0
<=> (2x+1)(2x-1-3x+5)=0
<=> (2x+1)(4-x)=0
<=>\([^{2x+1=0}_{4-x=0}< =>[^{2x=-1}_{x=4}< =>[^{x=\frac{-1}{2}}_{x=4}\)
2) (x+1)2= 4(x2-2x+1)
<=> x2+2x+1-4(x2-2x+1)=0
<=> x2+2x+1-4x2+8x-4=0
<=> -3x2+10x-3=0
<=> -3x2+x+9x-3=0
<=> -x(3x-1)+3(3x-1)=0
<=> (3x-1)(3-x)=0
<=> \([^{3x-1=0}_{3-x=0}< =>[^{3x=1}_{x=3}< =>[^{x=\frac{1}{3}}_{x=3}\)
3) 2x3+5x2-3x=0
<=> 2x(x2+\(\frac{5}{2}x-\frac{3}{2})=0\)
<=> 2x\(\left[x^2+2.\frac{5}{4}x+\frac{25}{16}-\left(\frac{25}{16}+\frac{3}{2}\right)\right]=0\)
<=> 2x\(\left[\left(x+\frac{5}{4}\right)^2-\frac{49}{16}\right]=0\)
<=> 2x\(\left(x+\frac{5}{4}-\frac{7}{4}\right)\left(x+\frac{5}{4}+\frac{7}{4}\right)=0\)
<=> x\(\left(x-\frac{1}{2}\right)\left(x+3\right)=0\)
<=>\(\left[{}\begin{matrix}x=0\\x=\frac{1}{2}\\x=-3\end{matrix}\right.\)
4) 2x=3x-2
<=> 2x-3x=-2
<=> -x=-2
<=> x=2
5) x+15=3x-1
<=> x-3x=1-15
<=> -2x=-14
<=> x=-14:-2
<=> x=7
6) 2-x=0,5x-4
<=> -x-0,5x=-4-2
<=> -1,5x=-6
<=> x= -6: -1,5
<=> x=4
học tốt nghen
KT
31 tháng 1 2018
a) \(\left(x-3\right)\left(6-x\right)>0\)
\(\Rightarrow\)\(\hept{\begin{cases}x-3>0\\6-x>0\end{cases}\Leftrightarrow\hept{\begin{cases}x>3\\x< 6\end{cases}\Leftrightarrow}3< x< 6}\)
hoặc \(\hept{\begin{cases}x-3< 0\\6-x< 0\end{cases}\Leftrightarrow\hept{\begin{cases}x< 3\\x>6\end{cases}}}\)(vô lí)
Vậy \(3< x< 6\)