Bài 1 : Cho a > b > 0 và 3a2 + 3b2 = 10ab . Tính P =\(\dfrac{a-b}{a+b}\)
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


1. b3+b= 3
(b3+b)=3
b.(3+1)=3
b. 4= 3
b=\(\dfrac{3}{4}\)
a3+a= 3 b3
(a3+a)=3
a.(3+1)=3
a. 4= 3
a=\(\dfrac{3}{4}\)
2

Xét: P2 = \(\dfrac{\left(a-b\right)^2}{\left(a+b\right)^2}=\dfrac{a^2-2ab+b^2}{a^2+2ab+b^2}=\dfrac{3a^2+3b^2-6ab}{3a^2+3b^2+6ab}=\dfrac{10ab-6ab}{10ab+6ab}=\dfrac{4ab}{16ab}=\dfrac{1}{4}\)
=> P = \(\dfrac{1}{2}\)

Ta có : \(3a^2+3b^2=10ab\)
\(\Leftrightarrow3a^2-ab-9ab+3b^2=0\)
\(\Leftrightarrow a\left(3a-b\right)-3b\left(3a-b\right)=0\)
\(\Leftrightarrow\left(3a-b\right)\left(a-3b\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}3a-b=0\\a-3b=0\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}b=3a\left(L\right)\\a=3b\left(N\right)\end{matrix}\right.\)
Thế \(a=3b\) vào P ta được :
\(P=\dfrac{3b-b}{3b+b}=\dfrac{2b}{4b}=\dfrac{1}{2}\)

Ta có : \(3a^2+3b^2=10ab\Rightarrow3a^2+3b^2-10ab=0\)
\(\Rightarrow\left(4a^2-8ab+4a^2\right)-\left(a^2+2ab+b^2\right)=0\)
\(\Rightarrow\left(2a-2b\right)^2=\left(a+b\right)^2\Rightarrow2a-2b=a+b\Rightarrow a=3b\)
\(\Rightarrow D=\dfrac{a-b}{a+b}=\dfrac{3b-b}{3b+b}=\dfrac{1}{2}\)

ta có 3a2 + 3b2 = 10ab
=> 3a2 + 3b2 - 9ab-ab = 0 => ( 3a2 - 9ab ) - ( ab - 3b2 )
=> ( a-3b ) (3a-b) = 0 => a=3b or 3a=b
vì b>a>0 => 3a = b
rùi bạn thay b bằng 3a rùi tính như thường thui
nhớ tick nghe chưa k là k giải nữa đâu
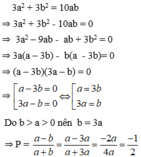
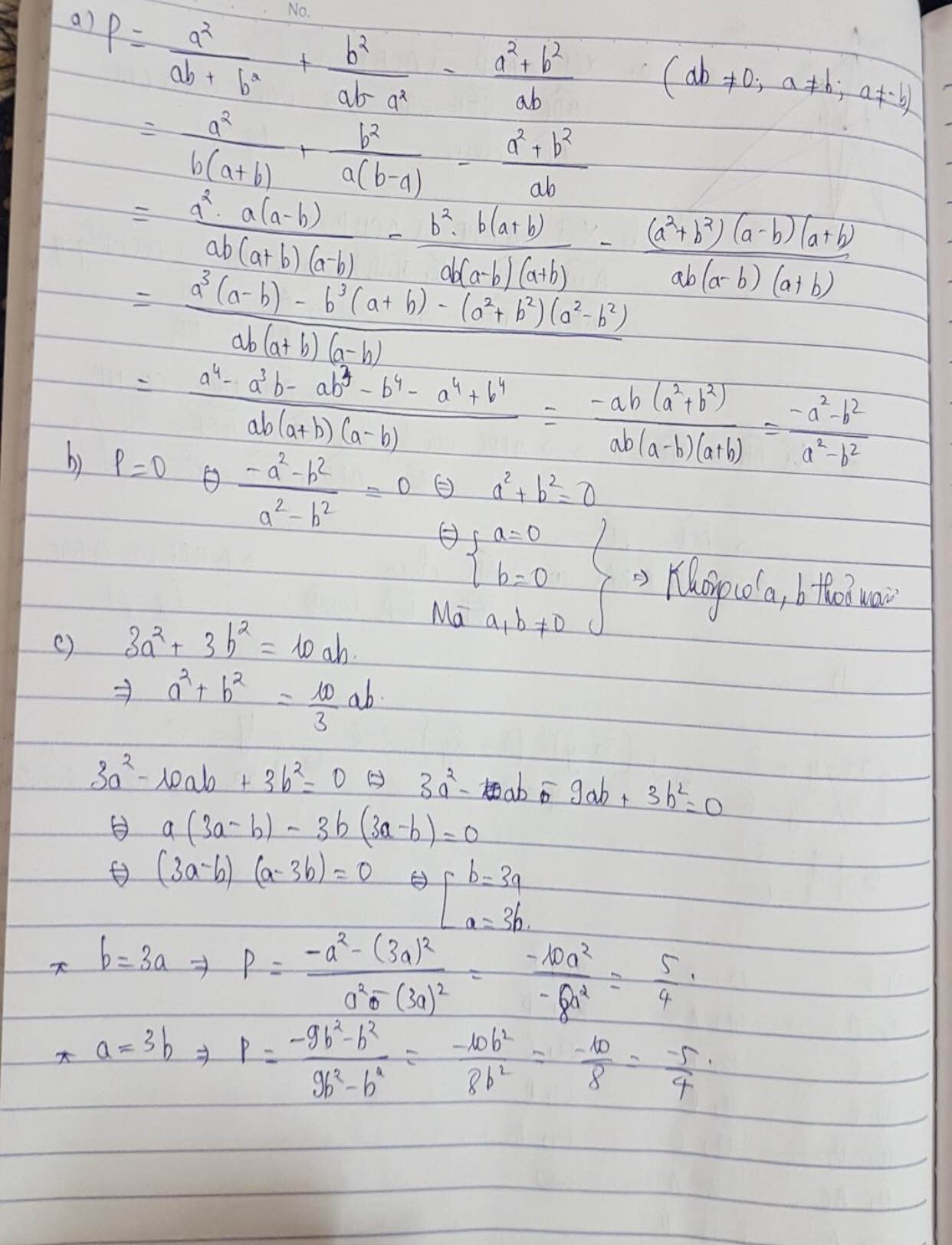
\(3a^2+3b^2=10ab\)
\(\Leftrightarrow\left(3a^2-9ab\right)+\left(3b^2-ab\right)=0\)
\(\Leftrightarrow3a\left(a-3b\right)+b\left(3b-a\right)=0\)
\(\Leftrightarrow\left(a-3b\right)\left(3a-b\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}a=3b\\a=\dfrac{1}{3}b\end{matrix}\right.\)
Vì a>b>0 nên a=3b
\(\Rightarrow P=\dfrac{a-b}{a+b}=\dfrac{3b-b}{3b+b}=\dfrac{2b}{4b}=\dfrac{1}{2}\)