So Sanh :
a) ( - 2 ) 201 và 0
b) ( - 2 ) 10và ( - 3 ) 25
c) 5a và 0 ; a ∈ Z
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
PN
1
31 tháng 12 2015
\(\frac{a}{b}=\frac{ad}{bd}>\frac{bc}{bd}=\frac{c}{d}\)
7 tháng 8 2017
\(\left(-333\right)^{2017}< 0\) (vì chữ số cuối của 2017 là lẻ)
\(\left(-15\right)^{2016}>0\)(vì chữ số cuối của 2016 là chẵn)
12 tháng 5 2023
3:
a: =>x=0 hoặc x+5=0
=>x=0 hoặc x=-5
b: =>x^2=4
=>x=2 hoặc x=-2
c: =>(x-5)(2x+1+x+6)=0
=>(x-5)(3x+7)=0
=>x=5 hoặc x=-7/3
MP
12 tháng 5 2023
1.
a. 2x - 6 > 0
\(\Leftrightarrow\) 2x > 6
\(\Leftrightarrow\) x > 3
S = \(\left\{x\uparrow x>3\right\}\)
b. -3x + 9 > 0
\(\Leftrightarrow\) - 3x > - 9
\(\Leftrightarrow\) x < 3
S = \(\left\{x\uparrow x< 3\right\}\)
c. 3(x - 1) + 5 > (x - 1) + 3
\(\Leftrightarrow\) 3x - 3 + 5 > x - 1 + 3
\(\Leftrightarrow\) 3x - 3 + 5 - x + 1 - 3 > 0
\(\Leftrightarrow\) 2x > 0
\(\Leftrightarrow\) x > 0
S = \(\left\{x\uparrow x>0\right\}\)
d. \(\dfrac{x}{3}-\dfrac{1}{2}>\dfrac{x}{6}\)
\(\Leftrightarrow\dfrac{2x}{6}-\dfrac{3}{6}>\dfrac{x}{6}\)
\(\Leftrightarrow2x-3>x\)
\(\Leftrightarrow2x-3-x>0\)
\(\Leftrightarrow x-3>0\)
\(\Leftrightarrow x>3\)
\(S=\left\{x\uparrow x>3\right\}\)
2.
a.
Ta có: a > b
3a > 3b (nhân cả 2 vế cho 3)
3a + 7 > 3b + 7 (cộng cả 2 vế cho 7)
b. Ta có: a > b
a > b (nhân cả 2 vế cho 1)
a + 3 > b + 3 (cộng cả 2 vế cho 3) (1)
Ta có; 3 > 1
b + 3 > b + 1 (nhân cả 2 vế cho 1b) (2)
Từ (1) và (2) \(\Rightarrow\) a + 3 > b + 1
c.
5a - 1 + 1 > 5b - 1 + 1 (cộng cả 2 vế cho 1)
5a . \(\dfrac{1}{5}\) > 5b . \(\dfrac{1}{5}\) (nhân cả 2 vế cho \(\dfrac{1}{5}\) )
a > b
3.
a. 2x(x + 5) = 0
\(\Leftrightarrow\left[{}\begin{matrix}2x=0\\x+5=0\end{matrix}\right.\) \(\Leftrightarrow\left[{}\begin{matrix}x=0\\x=-5\end{matrix}\right.\)
\(S=\left\{0,-5\right\}\)
b. x2 - 4 = 0
\(\Leftrightarrow x\left(x-4\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}x=0\\x-4=0\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=0\\x=4\end{matrix}\right.\)
\(S=\left\{0,4\right\}\)
d. (x - 5)(2x + 1) + (x - 5)(x + 6) = 0
\(\Leftrightarrow\left(x-5\right)\left(2x+1+x+6\right)=0\)
\(\Leftrightarrow\left(x-5\right)\left(3x+7\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}x-5=0\\3x+7=0\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=5\\x=\dfrac{-7}{3}\end{matrix}\right.\)
\(S=\left\{5,\dfrac{-7}{3}\right\}\)
CM
16 tháng 10 2019
Ta có: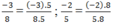 
Vì (-3).5 > 8 . (-2) nên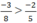 
Với hai phân số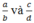 
(a, b, c, d ∈ Z ; b > 0 ; d > 0) nếu 
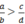thì ad > bc hoặc 
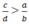thì cb > ad
Ta chứng minh: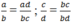 
Ta có: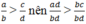 
Theo quy tắc so sánh hai phân số ta có: ad > bc
Theo chiều ngược lại, ta cũng có:
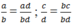
Theo quy tắc so sánh hai phân số nếu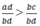 
Suy ra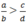 
G
0
a) ta có \(\left(-2\right)^{201}\)<0(vì -2 là số nguyên âm có số mũ lẻ là 201)
b)Ta có \(\left(-2\right)^{10}=2^{10}\)>0;\(\left(-3\right)^{25}< 0\)(-3 là số nguyên âm với số mũ lẻ)
\(\Rightarrow\left(-2\right)^{10}>\left(-3\right)^{25}\)
c)5a và 0 a\(\in Z\)
Trường hợp 1:a>0
Với a >o ta có : 5 .a =5.(0+x).0(x\(\in N\))
Trường hợp 2:a<0
với a<0 ta có 5a =5.(0-x)<0(x\(\in N\))
Trường hợp 3:a=0
Với a=0 ta có 5a=5.0=0