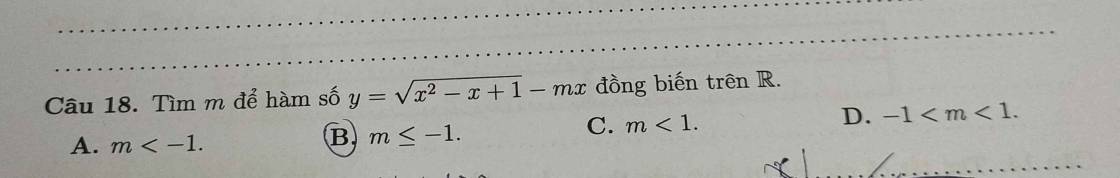Mình đg cần gấp
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


a) Ta có: \(Q=\dfrac{3x+\sqrt{9x}-3}{x+\sqrt{x}-2}-\dfrac{\sqrt{x}+1}{\sqrt{x}+2}+\dfrac{\sqrt{x}-2}{1-\sqrt{x}}\)
\(=\dfrac{3x+3\sqrt{x}-3-\left(x-1\right)-\left(x-4\right)}{\left(\sqrt{x}+2\right)\left(\sqrt{x}-1\right)}\)
\(=\dfrac{3x+3\sqrt{x}-3-x+1-x+4}{\left(\sqrt{x}+2\right)\left(\sqrt{x}-1\right)}\)
\(=\dfrac{x+3\sqrt{x}+2}{\left(\sqrt{x}+2\right)\left(\sqrt{x}-1\right)}\)
\(=\dfrac{\sqrt{x}+1}{\sqrt{x}-1}\)
b) Thay \(x=4+2\sqrt{3}\) vào Q, ta được:
\(Q=\dfrac{\sqrt{3}+1+1}{\sqrt{3}+1-1}=\dfrac{2+\sqrt{3}}{\sqrt{3}}=\dfrac{2\sqrt{3}+3}{3}\)
c) Để Q=3 thì \(\sqrt{x}+1=3\sqrt{x}-3\)
\(\Leftrightarrow\sqrt{x}-3\sqrt{x}=-3-1\)
\(\Leftrightarrow2\sqrt{x}=4\)
hay x=4
d) Để \(Q>\dfrac{1}{2}\) thì \(\dfrac{\sqrt{x}+1}{\sqrt{x}-1}-\dfrac{1}{2}>0\)
\(\Leftrightarrow\dfrac{2\sqrt{x}+2-\sqrt{x}+1}{2\left(\sqrt{x}-1\right)}>0\)
\(\Leftrightarrow\sqrt{x}-1>0\)
\(\Leftrightarrow x>1\)
Kết hợp ĐKXĐ, ta được: x>1
e) Để Q nguyên thì \(\sqrt{x}+1⋮\sqrt{x}-1\)
\(\Leftrightarrow2⋮\sqrt{x}-1\)
\(\Leftrightarrow\sqrt{x}-1\in\left\{-1;1;2\right\}\)
\(\Leftrightarrow\sqrt{x}\in\left\{0;2;3\right\}\)
hay \(x\in\left\{0;4;9\right\}\)

Cơ chế hình thành cây có kiểu gen Aaa là do rồi loạn giảm phân, diễn ra ở kì sau của giảm phân 1.
Sơ đồ lai:
P: Aa x Aa
GP: Aa ; 0 ; A ; a
F1: Aaa ; a

1 I'm not really interested in robotics.
2 We might go to the moon for our summer holiday in 2050.
3 I couldn't email you last night because my computer didn't work.
4 I didn't need to finish my homework yesterday.
5 She has worked at the school canteen for two months.
6 If you don't study hard, you won't pass the exam.




\(\left(x^2-1\right)'=2x;\left[\left(x-2\right)^4\right]'=4\cdot\left(x-2\right)^3\cdot\left(x-2\right)'=4\left(x-2\right)^3\)
\(f''\left(x\right)=\left(x^2-1\right)'\left(x-2\right)^4+\left(x^2-1\right)\left[\left(x-2\right)^4\right]'\)
\(=2x\left(x-2\right)^4+\left(x^2-1\right)\cdot4\left(x-2\right)^3\)
\(=2\left(x-2\right)^3\left[x\left(x-2\right)+2x^2-2\right]\)
\(=2\left(x-2\right)^3\left(3x^2-2x-2\right)\)
Đặt \(f'\left(x\right)=0\)
=>\(\left[{}\begin{matrix}x=1\\x=-1\\x=2\end{matrix}\right.\)
\(f''\left(2\right)=0;f''\left(1\right)=2>0;f''\left(-1\right)=-162< 0\)
=>Chọn B


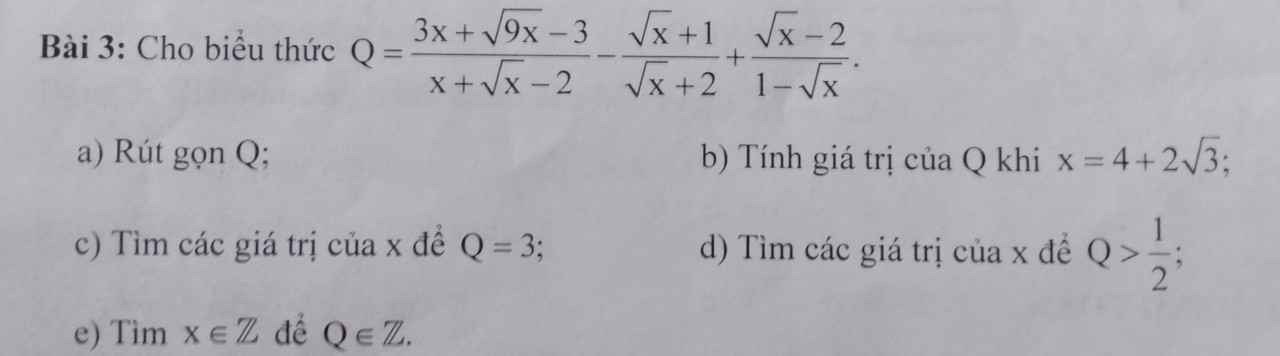 giúp mình vs mình đg cần gấp
giúp mình vs mình đg cần gấp