Question

[Đặng Cẩm Vân]

Cho \(\Delta ABC\). Gọi E, F theo thứ tự là trung điểm của các cạnh AB, AC. Trên tia đối của FB lấy điểm P sao cho PF=BF. Trên tia đối của tia EC lấy điểm Q sao cho QE=CE.

a, Chứng minh AP=AQ

b, Chứng minh 3 điểm P,A,Q thẳng hàng

c, Chứng minh BQ//AC và CP//AC

d, Gọi R là giao điểm của 2 đường thẳng PC và QB. Chứng minh rằng chu vi của \(\Delta PQR\) bằng 2 lần chu vi của \(\Delta ABC\)

e, Chứng minh 3 đường thẳng AR, BP, CQ đồng quy tại 1 điểm

Answer 1

[Nguyễn Lê Phước Thịnh]

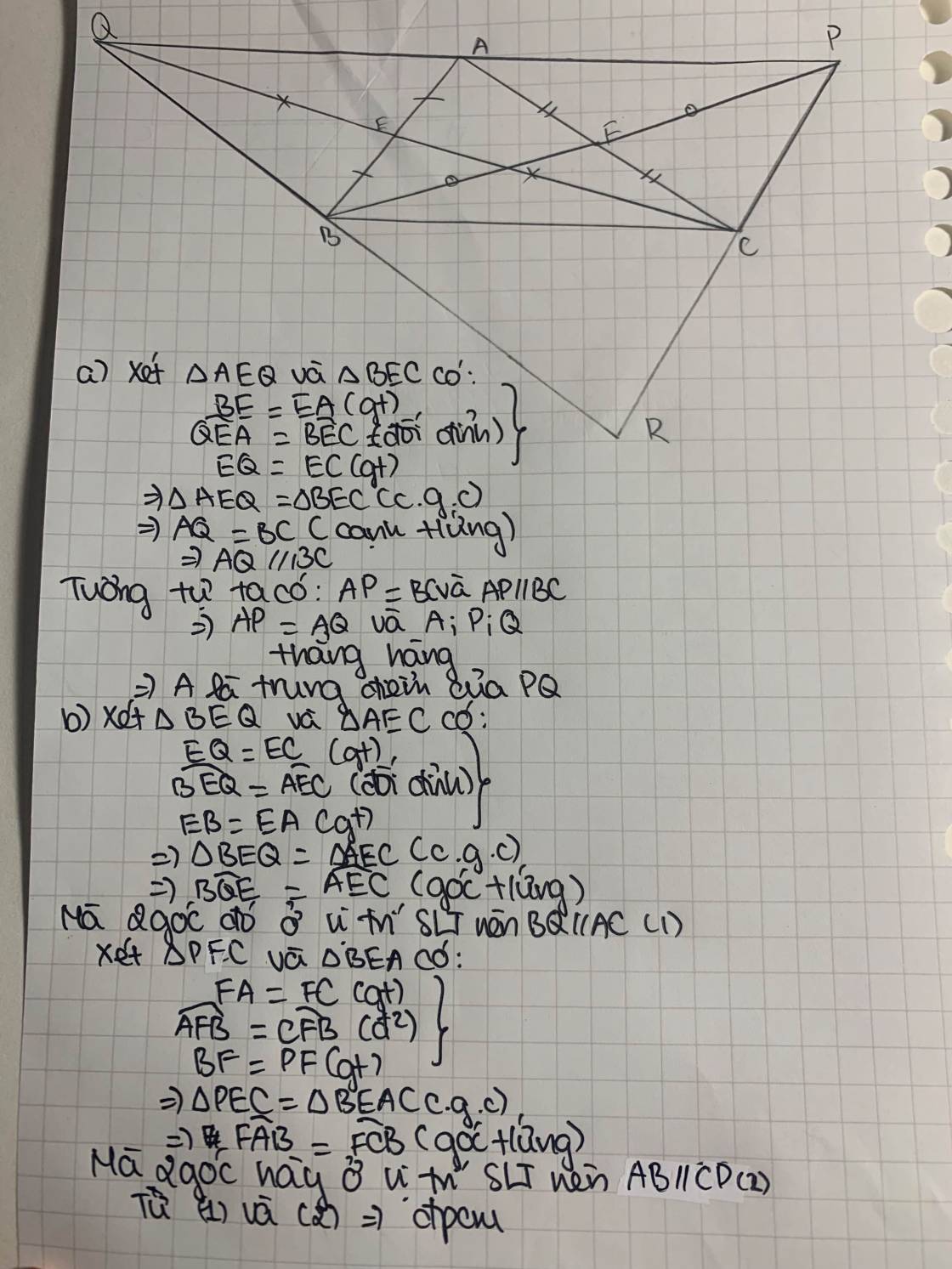
a: Xét tứ giác ABCP có 

F là trung điểm của AC
F là trung điểm của BP

Do đó: ABCP là hình bình hành

Suy ra: AP//BC và AP=BC(1)

Xét tư sgiác AQBC có 

E là trung điểm của AB

E là trung điểm của QC

Do đó:AQBC là hình bình hành

Suy ra: AQ//BC và AQ=BC(2)

Từ (1) và (2) suy ra AP=AQ

b: Ta có: AP//BC

AQ//BC

AP,AQ có điểm chung là A

Do đó: A,P,Q thẳng hàng

c: Ta có: AQBC là hình bình hành

nên BQ//AC

Ta có: ABCP là hình bình hành

nên CP//AB