Cho đoạn thẳng AB, vẽ về 1 phía của AB các tia Ax, By vuông góc vs AB. Gọi C là điểm bất kì thuộc AB, gọi D,E theo thứ tự là các điểm bất kì thuộc tia Ax, By. CMR: CDA+CEB=DCE Thankss
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Những câu hỏi liên quan

30 tháng 8 2017
Câu này hơi kì, vì đề đã nói rõ tiếp tuyến cắt Oz tại M, thế thì M chạy trên tia Oz còn hỏi gì nữa???
mình nghĩ câu này, nên "giấu" cái Oz đi, mà cho M là trung điểm của CD, làm thế nhé
Thấy tứ giác ABDC là hình thang vuông, có OM là đường trung bình (qua trung điểm 2 cạnh bên)
=> OM // Ax // By => M chạy trên tia qua O và // Ax (chính là Oz)

28 tháng 10 2023
a: Xét ΔDAC vuông tại A và ΔCBE vuông tại B có
DA=CB
AC=BE
Do đó: ΔDAC=ΔCBE
b: ΔDAC=ΔCBE
=>\(\widehat{DCA}=\widehat{CEB}\)
=>\(\widehat{DCA}+\widehat{ECB}=90^0\)
\(\widehat{DCA}+\widehat{DCE}+\widehat{BCE}=180^0\)(hai góc kề bù)
=>\(\widehat{DCE}+90^0=180^0\)
=>\(\widehat{DCE}=90^0\)
=>CD\(\perp\)CE
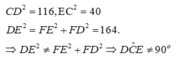
Xét tam giác ADC vuông tại A và tam giác EBC vuông tại B có:
\(\left\{{}\begin{matrix}\widehat{ADC}=90^0-\widehat{ACD}\\\widehat{CEB}=90^0-\widehat{ECB}\end{matrix}\right.\)
\(\Rightarrow\widehat{ADC}+\widehat{CEB}=90^0-\widehat{ACD}+90^0-\widehat{ECB}=180^0-\left(\widehat{ACD}+\widehat{ECB}\right)=180^0-\left(180^0-\widehat{DCE}\right)=\widehat{DCE}\left(đpcm\right)\)