Tính thể tích V của vật đk tảoa khi quay hình giới hạn bởi đường y mũ 2 = ( x -1)mũ 3 và đường x = 2 quanh trục Ox
giúp mk vs
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Thể tích vật thể tròn xoay cần tìm là
V = π ∫ 0 2 x 2 dy = π ∫ 0 2 y 4 dy = 32 π 5
Đáp án B

Thể tích vật thể tròn xoay sinh ra bởi miền CED quay quanh trục Ox là hiệu của hai thể tích ( V 1 và V 2 ) của hai vật thể tròn xoay tương ứng sinh ra khi miền ACEB và miền ACDB quay quanh trục Ox. Như vậy V = V 1 – V 2 , trong đó :

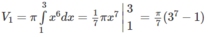
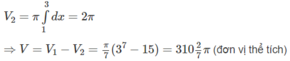

Chọn D
D quay xung quanh trục Oy
Ta có: y = ( x - 2 ) 2 ⇔ x - 2 = ± y ⇔ x = 2 ± y
V = π ∫ 0 4 2 + y 2 - 2 - y 2 dy = 8 π . ∫ 0 4 y dy = 8 π . 2 3 y 3 2 | 0 π = 128 π 3 đ v t t

Đáp án B.
Thể tích vật thể cần tính là:
V = π ∫ 1 a 1 x 2 d x = π ∫ 1 a d x x 2 = − π x a 1 = π − π a .