Question

[Giang Đàm]

Mn giải hộ mình bài nè với

Answer 1

[T.Thùy Ninh]

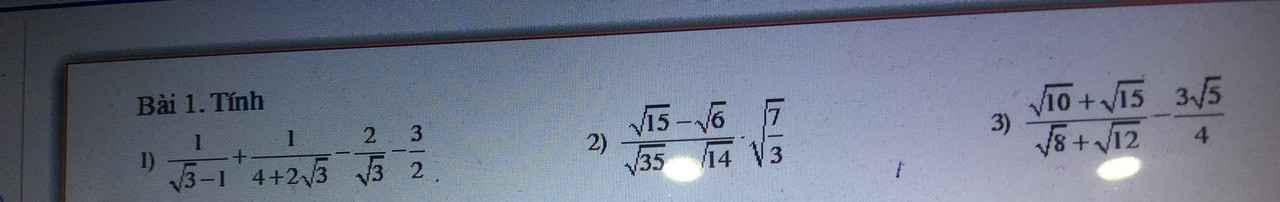
Vì tam giác ABC vuông tại A \(\Rightarrow BC^2=AB^2+AC^2\)

\(\Leftrightarrow BC^2=36+64=100\Rightarrow BC=\sqrt{100}=10cm\)Vì AD là tia phân giác của tam giác ABC

\(\Rightarrow\dfrac{DB}{AB}=\dfrac{DC}{AC}\)

Áp dụng tính chất dãy tỉ số bằng nhau ta có:

\(\dfrac{DB}{AB}=\dfrac{DC}{AC}=\dfrac{DB+DC}{AC+AB}=\dfrac{BC}{6+8}=\dfrac{10}{14}=\dfrac{5}{7}\)\(\Rightarrow DB=\dfrac{5}{7}.6=\dfrac{30}{7}cm\)

\(DC=\dfrac{5}{7}.8=\dfrac{40}{7}cm\)

b, Xét tam giác ABC và HBD có:

\(\widehat{BHD}=\widehat{BAC}\)

\(\widehat{B}\) là góc chung

\(\Rightarrow\) tam giác ABC ~ HBD

\(\Rightarrow\dfrac{AC}{BC}=\dfrac{HD}{BD}\Rightarrow HD=\dfrac{AC.BD}{BC}=\dfrac{8.\dfrac{30}{7}}{10}=\dfrac{24}{7}cm\)Xét tam giác vuông HDC có:

\(BH^2=BD^2-DH^2=\left(\dfrac{30}{7}\right)^2-\left(\dfrac{24}{7}\right)^2=\dfrac{324}{49}\Rightarrow BH=\dfrac{18}{7}cm\)\(\Rightarrow HA=AB-BH=6-\dfrac{18}{7}=\dfrac{24}{7}cm\)

Xét tam giác vuông HDA có:

\(AD^2=DH^2+HA^2=\left(\dfrac{24}{7}\right)^2+\left(\dfrac{24}{7}\right)^2=\dfrac{1152}{49}\Rightarrow AD=\sqrt{\dfrac{1152}{49}}=\dfrac{24\sqrt{2}}{7}\)

Answer 2

[T.Thùy Ninh]

Bài 2.

Vẽ AH vuông góc với BC

Vì ABC là tam giác vuông \(\Rightarrow AC^2=BC^2-AB^2=144\Rightarrow AC=\sqrt{144}=12cm\)

Vì AD là tia phân giác của tam giác ABC \(\Rightarrow\dfrac{DB}{AB}=\dfrac{DC}{AC}\)

Áp dụng dãy tỉ số bằng nhau ta có:

\(\dfrac{DB}{AB}=\dfrac{DC}{AC}=\dfrac{DB+DC}{AB+AC}=\dfrac{BC}{5+12}=\dfrac{13}{17}\Rightarrow BD=\dfrac{13}{17}.5=\dfrac{65}{17}cm\)Tỉ số diện tích:

\(\dfrac{S_{ABD}}{S_{ABC}}=\dfrac{\dfrac{1}{2}AH.DB}{\dfrac{1}{2}AH.BC}=\dfrac{DB}{BC}=\dfrac{\dfrac{65}{17}}{13}=\dfrac{5}{17}\)