Tìm GTNN của biểu thức: 4a2 +4a +2
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
CM
3 tháng 3 2017
Đáp án đúng : A
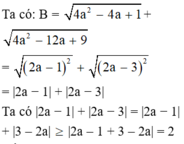
Dấu “=” xảy ra ⇔ 2 a − 1 3 − 2 a ≥ 0 ⇔ 1 2 ≤ a ≤ 3 2
Vậy GTNN của B là 2 khi 1 2 ≤ a ≤ 3 2
CM
8 tháng 6 2017
a) M có nghĩa khi a 3 - 4 a ≠ 0 ⇔ a ≠ { 0 ; ± 2 }
b) Rút gọn thu được: M = a ( a 2 + 4 a + 4 ) a ( a 2 − 4 ) = a + 2 a − 2
c) M = − 3 ⇔ a + 2 a − 2 = − 3 ⇔ a = 1 (TMĐK)
TP
2
P
20 tháng 11 2017
A=(a4-2a3+a2) +2(a2-2a+1) +3
=(a2-a)2 + 2(a-1)2 + 3 \(\ge\)3
Dấu bằng xay ra khi a=1
20 tháng 11 2017
A=a4 -2a3 +3a2 -4a +5
=a4 -2a3 +a2 +2a2-4a+2+3
=(a4 -2a3 +a2) +2(a2 -2a +1)+3
=(a2-a)2 +2(a-1)2 +3
\(\hept{\begin{cases}\left(a^2-a\right)^2\ge3\\2\left(a-1\right)^2\ge3\end{cases}\Rightarrow A_{Min}=3}\)
NT
7
17 tháng 1 2017
2a=x
2b=y
cho gọn hệ số
\(\Leftrightarrow x^2+xy+y^2-6x-6y+12\\ \\\)
\(\left(x+\frac{y}{2}-3\right)^2+\left(y^2-6y+12\right)-\left(\frac{y^2}{4}-3y+9\right)\) để nguyên lại cho bạn dẽ hiểu
\(\left(x+\frac{y}{2}-3\right)^2+\frac{3}{4}\left(y-2\right)^2\ge0\)đẳng thức khi y=2; x=2=> a=b=4
BH
17 tháng 1 2017
Bác Ngô Như Minh giải đúng rồi. Nhầm một tí ở đoạn cuối cùng, đó là a = b = 1 mới đúng.
Tuy nhiên chỗ đó không quan trọng lắm. Nhầm lẫn là chuyện bình thường.
Ủng hộ bác Minh vác Kiếm tung hoành thiên hạ. Em chọn đúng rồi đấy.
PN
27 tháng 8 2020
Bài 1
a) \(\left(x+1\right)^3+\left(x-1\right)^3+x^3-3x\left(x-1\right)\left(x+1\right)\)
\(=x^3+3x^2+3x+1+x^3-3x^2+3x-1+x^3-3x\left(x^2-1\right)\)
\(=3x^3+6x-3x^3+3x=9x\)
b) \(\left(a+b+c\right)^2+\left(a+b-c\right)^2+\left(2a-b\right)^2\)
\(=a^2+b^2+c^2+2\left(ab+bc+ca\right)+a^2+b^2+c^2+2ab-2bc-2ca+4a^2-4ab+b^2\)
\(=6a^2+3b^2+2c^2+4ab-4ab=6a^2+3b^2+2c^2\)
Bài 2
a) \(x^2-20x+101=\left(x^2-20x+100\right)+1=\left(x-10\right)^2+1\ge1\)
Dấu = xảy ra \(< =>\left(x-10\right)^2=0< =>x-10=0< =>x=10\)
b) \(4a^2+4a+2=4\left(a^2+a+\frac{1}{4}\right)+1=4\left(a+\frac{1}{2}\right)^2+1\ge1\)
Dấu = xảy ra \(< =>4\left(a+\frac{1}{2}\right)^2=0< =>a+\frac{1}{2}=0< =>a=-\frac{1}{2}\)
c) \(x^2-4xy+5y^2+10x-22y+28=\left(x^2-4xy+4y^2\right)+10\left(x-2y\right)+y^2-2y+1+27\)
\(=\left(x-2y\right)^2+2.5.\left(x-2y\right)+25+\left(y-1\right)^2+2\)
\(=\left(x-2y+5\right)^2+\left(y-1\right)^2+2\ge2\)
Dấu = xảy ra \(< =>\hept{\begin{cases}y-1=0\\x-2y+5=0\end{cases}< =>\hept{\begin{cases}y=1\\x=-3\end{cases}}}\)
Bài 3
a) \(4x-x^2+3=-\left(x^2-4x+4\right)+7=-\left(x-2\right)^2+7\le7\)
Dấu = xảy ra \(< =>\left(x-2\right)^2=0< =>x-2=0< =>x=2\)
b) \(x-x^2=-\left(x^2-x+\frac{1}{4}\right)+\frac{1}{4}=-\left(x-\frac{1}{2}\right)^2+\frac{1}{4}\le\frac{1}{4}\)
Dấu = xảy ra \(< =>\left(x-\frac{1}{2}\right)^2=0< =>x-\frac{1}{2}=0< =>x=\frac{1}{2}\)
Biểu thức được biến đổi thành:
\(=\left(2a\right)^2+2.2a+1+1\)
\(=\left(2a+1\right)^2+1\)
Đặt biểu thức trên là A, ta có:
\(\left(2x+1\right)\ge0=>MinA=1\) khi (2x-1) = 0 => \(x=\dfrac{1}{2}\)
Vậy giá trị nhỏ nhất của biểu thức là 1;
Chúc bạn học tốt.......