Cho 2x=8y+1và9y=3x-9 (x;y thuộc N).Tính x+y
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
15 tháng 10 2021
a: \(2x\left(x^2-3x+1\right)=2x^3-6x^2+2x\)
b: \(\left(x+2\right)^2-x^2=4x+4\)
c: \(\left(x+3\right)\left(x^2-3x+9\right)-x^3=27\)
K
1
18 tháng 10 2021
TL
x=3/4-3*căn bậc hai(5)/4, x=3*căn bậc hai(5)/4+3/4
-y^2+8*y-x^2+2*x+15
-y^2+7*y-x^2+3*x+21
-y^2+(2*x+12)*y-x^2-4*x+45
HT
KV
30 tháng 10 2023
a) 3x³ + 6x²y
= 3x².(x + 2y)
b) 2x³ - 6x²
= 2x².(x - 2)
c) 18x² - 20xy
= 2x.(9x - 10y)
d) xy + y² - x - y
= (xy + y²) - (x + y)
= y(x + y) - (x + y)
= (x + y)(y - 1)
e) (x²y² - 8)² - 1
= (x²y² - 8 - 1)(x²y² - 8 + 1)
= (x²y² - 9)(x²y² - 7)
= (xy - 3)(xy + 3)(x²y² - 7)
f) x² - 7x - 8
= x² - 8x + x - 8
= (x² - 8x) + (x - 8)
= x(x - 8) + (x - 8)
= (x - 8)(x + 1)
30 tháng 10 2023
a: \(3x^3+6x^2y\)
\(=3x^2\cdot x+3x^2\cdot2y=3x^2\left(x+2y\right)\)
b: \(2x^3-6x^2=2x^2\cdot x-2x^2\cdot3=2x^2\left(x-3\right)\)
c: \(18x^2-20xy=2x\cdot9x-2x\cdot10y=2x\left(9x-10y\right)\)
d: \(xy+y^2-x-y\)
\(=y\left(x+y\right)-\left(x+y\right)\)
\(=\left(x+y\right)\left(y-1\right)\)
e: \(\left(x^2y^2-8\right)^2-1\)
\(=\left(x^2y^2-8-1\right)\left(x^2y^2-8+1\right)\)
\(=\left(x^2y^2-7\right)\left(x^2y^2-9\right)\)
\(=\left(x^2y^2-7\right)\left(xy-3\right)\left(xy+3\right)\)
f: \(x^2-7x-8\)
\(=x^2-8x+x-8\)
\(=x\left(x-8\right)+\left(x-8\right)=\left(x-8\right)\left(x+1\right)\)
g: \(10x^2\left(2x-y\right)+6xy\left(y-2x\right)\)
\(=2x\cdot\left(2x-y\right)\cdot5x-2x\cdot\left(2x-y\right)\cdot3y\)
\(=2x\left(2x-y\right)\left(5x-3y\right)\)
h: \(x^2-2x+1-y^2\)
\(=\left(x-1\right)^2-y^2\)
\(=\left(x-1-y\right)\left(x-1+y\right)\)
i: \(2x\left(x+2\right)+x^2\left(-x-2\right)\)
\(=2x\left(x+2\right)-x^2\left(x+2\right)\)
\(=\left(x+2\right)\left(2x-x^2\right)=x\cdot\left(x+2\right)\left(2-x\right)\)
k: \(-x^2+6x-9=-\left(x^2-6x+9\right)\)
\(=-\left(x^2-2\cdot x\cdot3+3^2\right)=-\left(x-3\right)^2\)
l: \(-2x^2+8xy-8y^2\)
\(=-2\left(x^2-4xy+4y^2\right)\)
\(=-2\left(x-2y\right)^2\)
m: \(3x^2+5x-3y^2-5y\)
\(=3\left(x^2-y^2\right)+5\left(x-y\right)\)
\(=3\left(x-y\right)\left(x+y\right)+5\left(x-y\right)\)
\(=\left(x-y\right)\left(3x+3y+5\right)\)
2 tháng 8 2023
6: =x^2-7xy+5xy-35y^2
=x(x-7y)+5y(x-7y)
=(x-7y)(x+5y)
7: =x^2-2xy-8xy+16y^2
=x(x-2y)-8y(x-2y)
=(x-2y)(x-8y)
8: =3x^2-6xy-4xy+8y^2
=3x(x-2y)-4y(x-2y)
=(x-2y)(3x-4y)
9: =4x^2+4xy+y^2-16y^2
=(2x+y)^2-16y^2
=(2x+y-4y)(2x+y+4y)
=(2x-3y)*(2x+5y)
10: =2(x^2+5xy+4y^2)
=2(x+y)(x+4y)
11: =5x(x+2y+y^2)
HS
2
28 tháng 12 2019
(x-2y-2)2+(y-6)2 =39-2A
A=< 39/2, max A là 39/2 khi x =14 và y =6
L
26 tháng 10 2019
\(a)xy+3x-2y=11\)
\(\Leftrightarrow xy+3x-2y-6=5\)
\(\Leftrightarrow x\left(y+3\right)-2\left(y+3\right)=5\)
\(\Leftrightarrow\left(y+3\right)\left(x-2\right)=5\)
\(\Leftrightarrow\hept{\begin{cases}y+3=-1\\x-2=-5\end{cases}}\Leftrightarrow\hept{\begin{cases}y=-4\\x=-3\end{cases}}\)
\(\Leftrightarrow\hept{\begin{cases}y+3=1\\x-2=5\end{cases}}\Leftrightarrow\hept{\begin{cases}y=-2\\x=7\end{cases}}\)
\(\Leftrightarrow\hept{\begin{cases}y+3=-5\\x-2=-1\end{cases}}\Leftrightarrow\hept{\begin{cases}y=-8\\x=1\end{cases}}\)
\(\Leftrightarrow\hept{\begin{cases}y+3=5\\x-2=1\end{cases}}\Leftrightarrow\hept{\begin{cases}y=2\\x=3\end{cases}}\)
L
26 tháng 10 2019
\(b)2x^2-2xy+x-y=12\)
\(\Leftrightarrow2x\left(x-y\right)+\left(x-y\right)=12\)
\(\Leftrightarrow\left(x-y\right)\left(2x+1\right)=12\)
\(\Rightarrow\left(x-y\right);\left(2x+1\right)\inƯ\left(12\right)\)
\(\RightarrowƯ\left(12\right)\in\left\{-1;1;-2;2;-3;3;-4;4;-6;6;-12;12\right\}\)
Vì 2x+1 luôn lẻ
\(\Rightarrow2x+1\in\left\{-1;1;-3;3\right\}\)
\(\Leftrightarrow\hept{\begin{cases}2x+1=-1\\x-y=-12\end{cases}}\Leftrightarrow\hept{\begin{cases}x=-1\\y=11\end{cases}}\)
\(\Leftrightarrow\hept{\begin{cases}2x+1=1\\x-y=12\end{cases}}\Leftrightarrow\hept{\begin{cases}x=0\\y=-12\end{cases}}\)
\(\Leftrightarrow\hept{\begin{cases}2x+1=-3\\x-y=-4\end{cases}}\Leftrightarrow\hept{\begin{cases}x=-2\\y=2\end{cases}}\)
\(\Leftrightarrow\hept{\begin{cases}2x+1=3\\x-y=4\end{cases}}\Leftrightarrow\hept{\begin{cases}x=1\\y=-3\end{cases}}\)
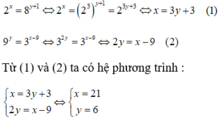
Ta có :
\(2^x=8^{y+1}=\left(2^3\right)^{y+1}=2^{3y+3}\)
\(\Rightarrow x=2y+3\left(1\right)\)
\(9^y=3^{x-9}\)
\(\Rightarrow\left(3^2\right)^y=3^{x-9}\)
\(\Rightarrow3^{2y}=3^{x-9}\)
\(\Rightarrow2y=x-9\)\(\left(2\right)\)
Từ \(\left(1\right)+\left(2\right)\Leftrightarrow x+2y=3y+3+x-9\)
\(\Rightarrow x+y=2y+x-6\)