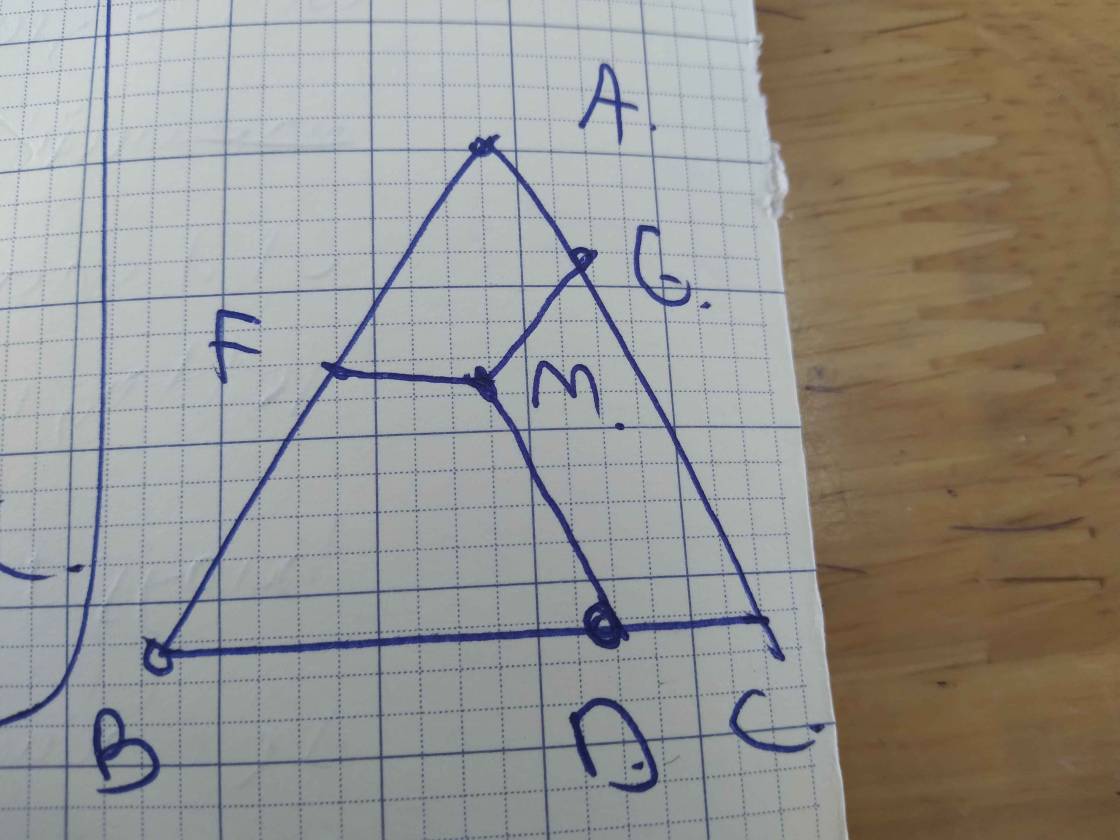
Cho tam giác ABC. Điểm M thuộc cạnh BC sao cho \(\dfrac{BM}{MC}=\dfrac{1}{2}\) . Qua M kẻ đường thẳng song song với AC cắt AB ở D. Qua M kẻ đường thẳng song song với AB cắt AC tại E. Tìm các cặp tam giác đồng dạng.
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
K
30 tháng 3 2020
Qua K vẽ đường thẳng // với AB cắt AC tại H.
=> AHKD là hình bình hành => DK = AH (1)
Gọi giao điểm của AK và DH là O. Vì AHKD là HBH => DO = OH
Xét 3 đường thẳng MA, CA, BA đồng quy tại A cắt 2 đường thẳng DH và BC ta được: DO/OH = BM/MC = 1
=> DH // BC (định lí chùm đường thẳng đồng quy đảo)
Xét ∆ ADH và ∆ FEC có:
AD = EF ( t/c đoạn chắn) ; DH = EC (t/c đoạn chắn) ; ^ADH = ^FEC => ∆ ADH = ∆ FEC (c-g-c)
=> AH = CF (2)
Từ (1) và (2) => CF = DK (đpcm)
GL
31 tháng 3 2020
Do EF//AB⇒\(\frac{CF}{CA}=\frac{EF}{AB}\)⇒\(\frac{CF}{EF}=\frac{AC}{AB}\)(1)
Dựng MG//AC và MM là trung điểm cạnh BC
⇒GM là đường trung bình ΔABC
=⇒G là trung điểm cạnh AB ⇒AG=BG
Do DK//GM⇒\(\frac{AD}{AG}=\frac{DK}{GM}\)⇒\(\frac{AD}{BG}=\frac{DK}{GM}\)
=> \(\frac{DK}{AD}=\frac{GM}{BG}=\frac{\frac{AC}{2}}{\frac{AB}{2}}=\frac{AC}{AB}\left(2\right)\)
Từ (1) và (2)\(\Rightarrow\frac{CF}{EF}=\frac{DK}{AD}\)
Mà tứ giác ADEF là hình bình hành (vì EF//AD và DE//AF) nên AD=EF
=> CF=DK (đpcm)
Nguồn: thuynga
3 tháng 2 2021
Ta có: \(\dfrac{MB}{MC}=\dfrac{1}{2}\)(gt)
nên MC=2MB
Ta có: MB+MC=BC(M nằm giữa B và C)
nên BC=2MB+MB=3MB
hay \(\dfrac{MB}{BC}=\dfrac{1}{3}\)
Xét ΔABC có
M∈BC(gt)
D∈AB(gt)
MD//AC(gt)
Do đó: ΔBMD\(\sim\)ΔBCA(Định lí tam giác đồng dạng)
⇒\(\dfrac{C_{BMD}}{C_{BCA}}=\dfrac{BM}{BC}\)(Tỉ số chu vi giữa hai tam giác đồng dạng)
\(\Leftrightarrow\dfrac{C_{BMD}}{24}=\dfrac{1}{3}\)
hay \(C_{DBM}=8\left(cm\right)\)
Ta có: \(\dfrac{MB}{MC}=\dfrac{1}{2}\)(gt)
nên \(MB=\dfrac{1}{2}MC\)
Ta có: MB+MC=BC(M nằm giữa B và C)
nên \(BC=\dfrac{1}{2}MC+MC=\dfrac{3}{2}MC\)
hay \(\dfrac{MC}{BC}=\dfrac{2}{3}\)
Xét ΔCBA có
M∈BC(gt)
E∈CA(Gt)
ME//AB(gt)
Do đó: ΔCME∼ΔCBA(Định lí tam giác đồng dạng)
\(\Leftrightarrow\dfrac{C_{CME}}{C_{CBA}}=\dfrac{CM}{CB}\)(Tỉ số chu vi giữa hai tam giác đồng dạng)
⇔\(\dfrac{C_{CME}}{24}=\dfrac{2}{3}\)
hay \(C_{CME}=\dfrac{48}{3}=16\left(cm\right)\)
Vậy: \(C_{DBM}=8\left(cm\right)\); \(C_{CME}=16\left(cm\right)\)
17 tháng 3 2020
Bài 6 :
Tự vẽ hình nhá :)
a) Gọi O là giao điểm của AC và EF
Xét tam giác ADC có :
EO // DC => AE/AD = AO/AC (1)
Xét tam giác ABC có :
OF // DC
=> CF/CB = CO/CA (2)
Từ (1) và (2) => AE/AD + CF/CB = AO/AC + CO/CA = AO + CO/AC = AC/AC = 1 => đpcm
Bài 7 :
a) Do EF // AB => CF / CA = EF / AB => CF / EF = AC / AB (1)
Dựng MG // AC và M là trung điểm của cạnh BC => GM là đường trung bình của tam giác ABC => G là trung điểm của cạnh AB =>AG = BG
Do DK // GM => AD / AG = DK / GM => AD / BG = DK / GM
=> DK / AD = GM / BG = \(\frac{\frac{AC}{2}}{\frac{AB}{2}}=\frac{AC}{AB} \left(2\right)\)
Từ (1) và (2) => CF / EF = DK / AD
Mà tứ giác ADEF là hình bình hành ( vì EF // AD và DE // AF ) nên AD = È
=> CF = DK ( đpcm )
Bài 8 :
Ta có : AB = AM + MB = 11 + 8 = 19 ( cm )
Áp dụng hệ quả định lí Ta-lét vào tam giác ABC, ta có :
AM / AB = AN / AC => AM + AB / AB = AN + AC / AC => 19 + 11 / 19 = AN + 38 / 38 => 30/19 = 38 + AN / 38
=> 1140 = 19.AN + 722
=> AN = ( 1140 - 722 ) / 19 = 22 ( cm )
=> NC = 38 - 12 = 26 ( cm )
3 tháng 3 2023
a: ΔCEF đồng dạng với ΔCAB theo tỉ số k=CE/CA
ΔADE đồng dạng với ΔABC
=>k'=AD/AB=2/5
b: \(\dfrac{C_{ADE}}{C_{ABC}}=\dfrac{AD}{AB}=\dfrac{2}{5}\)
=>\(C_{ADE}=\dfrac{2}{5}\cdot\left(5+7+9\right)=\dfrac{2}{5}\cdot21=\dfrac{42}{5}\left(cm\right)\)
ΔCEF đồng dạng với ΔCAB
=>\(\dfrac{C_{CEF}}{C_{CAB}}=\dfrac{CE}{CA}=\dfrac{3}{5}\)
=>\(C_{CEF}=\dfrac{3}{5}\cdot\left(5+7+9\right)=\dfrac{3}{5}\cdot21=\dfrac{63}{5}\left(cm\right)\)