Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
a) đổi 30 phút = 0,5h
sau 30 phút, xe đạp đi dc : 15 . 0,5 = 7,5km
sau 30 phút, xe máy đi dc : 30 . 0,5 = 15km
vì xe máy nghỉ 30 phút nhưng xe đạp vẫn đi => 30 phút đó xe đạp đi dc 1 đoạn là :
15 . 0,5 = 7.5km
vậy khoảng cách của 2 xe lúc này là :
7.5 + 7.5 + 15 = 30km
gọi s1,v1; s2,v2 lần lượt là quãng đường và vận tốc của xe máy và xe đạp. gọi t là thời gian 2 xe gặp nhau kể từ lúc 2 xe cách nhau 30km. lúc này 2 xe đi cùng chiều nên ta có
s1 = v1 . t
s2 = v2 . t
=> s1 - s2 = S ( S là khoảng cách của 2 xe lúc này = 30km)
=> v1 . t - v2 . t = t .( v1 - v2 ) = 30km
=> t . ( 30 - 15 ) = 30km
=> t = 2h
vậy 2 xe gặp nhau sau :
2 + 0,5 + 0,5 = 3h
b) vị trí gặp nhau cách A số km là:
15 . 3 = 45km
( tích mình nha, đúng r bạn)
1h người đi xe đạp đi được: \(S_1=10.1=10km\)
1h30' người đi bộ đi được: \(S_2=\dfrac{5.3}{2}=7,5km\)
Hai người cách nhau:
\(10+7,5=17,5km\)
Gọi t là thời gian 2 người gặp nhau (t>0)
Ta có phương trình:
\(10t-5t=17,5\)
\(t=3,5\left(TM\right)\)
Vậy sau 5h người đi xe đạp đuổi kịp người đi bộ
ta có:
quãng đường người đi xe đạp đi được tính từ lúc đi tới lúc nghỉ xong là:
\(S'=v_1.1=10km\)
quãng đường người đi bộ đi được tính từ lúc người đi xe đạp nghỉ xong là:
\(S''=1,5v_2=7,5km\)
khoảng cách hai người khi xe đạp quay lại đuổi người đi bộ là:
\(\Delta S=S'+S''=17,5km\)
ta lại có:
lúc người đi xe đạp đuổi kịp người đi bộ là:
\(S_1-S_2=\Delta S\)
\(\Leftrightarrow v_1t_1-v_2t_2=17,5\)
\(\Leftrightarrow10t_1-5t_2=17,5\)
mà t1=t2=t
\(\Rightarrow5t=17,5\Rightarrow t=3,5h\)
ủa sao s1-s2 lại là△s vậy
tui thấy △s là đoạn lớn nhất nên phải cộng chứ bạn
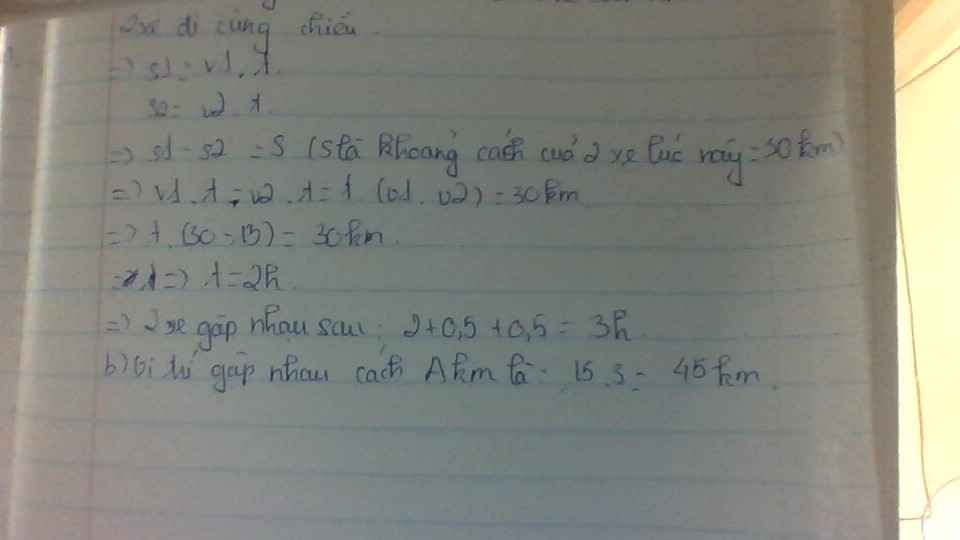
Đổi \(30'=0,5h\)
a, Quãng đường xe đạp đi được trong \(30'\)đầu là:
\(S_1=t_1.V_1=15.0,5=7,5\left(km\right)\)
Quãng đường xe máy đi được trong \(30'\)đầu là:
\(S_2=t_1.V_2=30.0,5=15\left(km\right)\)
Khi xe máy nghỉ \(30'\) thì xe đạp đi được :
\(S_3=t_2.V_1=0,5.15=7,5\left(km\right)\)
Khoảng cách của xe máy và xe đạp khi đó là:
\(S_4=S_1+S_2+S_3=7,5+15+7,5=30\left(km\right)\)
Thời gian để xe máy đuổi kịp xe đạp là:
\(t=\dfrac{S_4}{V_2-V_1}=\dfrac{30}{30-15}=\dfrac{30}{15}=2\left(h\right)\)
b, Chỗ gặp nhau cách A là:
\(S_5=t.V_1=2.15=30\left(km\right)\)
Bài giải:
a) Đổi 30 phút = 0,5 giờ
Sau 30 phút thì xe đạp đi được là:
15. 0,5 = 7,5 (km)
Sau 30 phút thì xe máy đi được là:
30. 0,5 = 15 (km)
Ta có: Xe máy nghỉ 30 phút nhưng xe đạp vẫn đi
=> Trong 30 phút đó xe đạp đi được là:
15. 0,5 = 7,5 (km)
Do đó: Khoảng cách của xe đạp và xe máy lúc này là:
7,5 + 7,5 + 15 = 30 (km)
Gọi s1, s2 ; v1, v2 lần lượt là quảng đường và vận tốc của xe máy, xe đạp
Và t là thời gian 2 xe gặp nhau kể từ lúc 2 xe cách nhau 30 km.
Vì lúc này 2 xe đi cùng chiều nhau
Nên ta có: s1 = v1. t và s2 = v2.t
Suy ra:
=> s1 - s2 = S (S là khoảng cách của 2 xe lúc này là 30 km)
=> v1.t - v2.t = t.(v1 - v2) = 30 (km)
=> t. (30 - 15) = 30 (km)
=> t = 2 (giờ)
Vậy hai xe gặp nhau sau thời gian là:
2 + 0,5 + 0,5 = 3 (giờ)
b) Vị trí gặp nhau cách A là:
15. 3 = 45 (km)
Chúc bạn học tốt!