1+21+32+43+................+10099+101100
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
16 tháng 10 2016
Ai cũng biết để tìm trung bình cộng của các số, chúng ta lấy tổng của các số rồi đem chia cho số số hạng.
Vậy đáp án A là đúng.
Mặc khác trong phép tính tìm trung bình cộng thì chắc chắn sẽ có dấu chia .
=> A là đúng
TM
16 tháng 10 2016
Trung cộng của 32; 43; 73 và 21 là :
( 32 + 43 + 73 + 21 ) : 4 = 118
=> Đáp án A đúng
CM
4 tháng 2 2019
Ta có: 10110 = (100+1)10 ( khai triển nhị thức Niu- tơn )
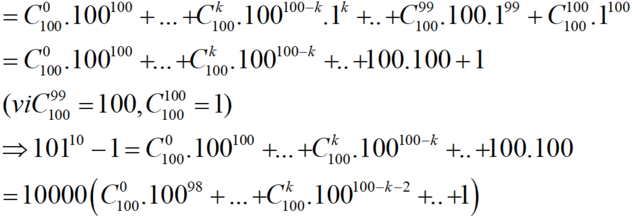
Do đó, 10110 -1 chia hết cho 10000
T
19 tháng 9 2023
\(C=1+3+3^2+3^3+\cdot\cdot\cdot+3^{11}\)
\(C=\left(1+3+3^2+3^3\right)+\left(3^4+3^5+3^6+3^7\right)+\left(3^8+3^9+3^{10}+3^{11}\right)\)
\(=\left(1+3+3^2+3^3\right)+3^4\left(1+3+3^2+3^3\right)+3^8\left(1+3+3^2+3^3\right)\)
\(=40+3^4\cdot40+3^8\cdot40\)
\(=40\cdot\left(1+3^4+3^8\right)\)
Vì \(40\cdot\left(1+3^4+3^8\right)⋮40\)
nên \(C⋮40\)
#\(Toru\)
19 tháng 9 2023
\(C=1+3+3^2+3^3+...+3^{11}\)
\(\Rightarrow C=\left(1+3+3^2+3^3\right)+3^4\left(1+3+3^2+3^3\right)+3^8\left(1+3+3^2+3^3\right)\)
\(\Rightarrow C=40+3^4.40+3^8.40\)
\(\Rightarrow C=40\left(1+3^4+3^8\right)⋮40\)
\(\Rightarrow dpcm\)
11 tháng 12 2015
bài này giống bài nào ý mk không nhớ nhưng hình như bạn là người trả lời
29 tháng 11 2021
15+21+32+43+54+65+76+87+98=471 em ko cắc chắn đâu vì em mới là học sinh lớp 2 thôi
8 tháng 10 2016
9342 chắc chắn 100000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000%
GN
GV Nguyễn Trần Thành Đạt
Giáo viên
1 tháng 8 2023
Bài 1:
\(2^{49}=\left(2^7\right)^7=128^7;5^{21}=\left(5^3\right)^7=125^7\\ Vì:128^7>125^7\Rightarrow2^{49}>5^{21}\)
Bài 2:
\(a,S=1+3+3^2+3^3+...+3^{99}\\ =\left(1+3+3^2+3^3\right)+3^4.\left(1+3+3^2+3^3\right)+...+3^{96}.\left(1+3+3^2+3^3\right)\\ =40+3^4.40+...+3^{96}.40\\ =40.\left(1+3^4+...+3^{96}\right)⋮40\\ b,S=1+4+4^2+4^3+...+4^{62}\\ =\left(1+4+4^2\right)+4^3.\left(1+4+4^2\right)+...+4^{60}.\left(1+4+4^2\right)\\ =21+4^3.21+...+4^{60}.21\\ =21.\left(1+4^3+...+4^{60}\right)⋮21\)
1 tháng 8 2023
Bài 1 :
\(2^{49}=\left(2^7\right)^7=128^7\)
\(5^{21}=\left(5^3\right)^7=125^7\)
mà \(125^7< 128^7\)
\(\Rightarrow2^{49}>5^{21}\)
Bài 2 :
a) \(S=1+3+3^2+3^3+...3^{99}\)
\(\Rightarrow S=\left(1+3+3^2+3^3\right)+3^4\left(1+3+3^2+3^3\right)...+3^{96}\left(1+3+3^2+3^3\right)\)
\(\Rightarrow S=40+40.3^4+...+40.3^{96}\)
\(\Rightarrow S=40\left(1+3^4+...+3^{96}\right)⋮40\)
\(\Rightarrow dpcm\)
b) \(S=1+4+4^2+4^3+...4^{62}\)
\(\Rightarrow S=\left(1+4+4^2\right)+4^3\left(1+4+4^2\right)+...4^{60}\left(1+4+4^2\right)\)
\(\Rightarrow S=21+4^3.21+...4^{60}.21\)
\(\Rightarrow S=21\left(1+4^3+...4^{60}\right)⋮21\)
\(\Rightarrow dpcm\)
15 tháng 8 2018
c, 64 * 25 + 35 * 25 + 25
= 64 * 25 + 35 * 25 + 25 * 1
= (64 + 35 + 1) * 25
= 100 * 25
= 2500
NM
Nguyễn Minh Quang
Giáo viên
11 tháng 12 2021
ta có
\(1+3+3^2+..+3^{2000}=\left(1+3+3^2\right)+\left(3^3+3^4+3^5\right)+..+\left(3^{1998}+3^{1999}+3^{2000}\right)\)
\(=13.1+13\cdot3^3+..+13\cdot3^{1998}\) chia hết cho 13
tương tự
\(1+4+4^2+..+4^{2012}=\left(1+4+4^2\right)+..+\left(4^{2010}+4^{2011}+4^{2012}\right)\)
\(=21.1+21\cdot4^3+..+21.4^{2010}\) chia hết cho 21
H9
HT.Phong (9A5)
CTVHS
26 tháng 10 2023
a) \(x+5=20-\left(12-7\right)\)
\(\Rightarrow x+5=20-5\)
\(\Rightarrow x+5=15\)
\(\Rightarrow x=15-5\)
\(\Rightarrow x=10\)
b) \(15-\left(3+2x\right)=2^2\)
\(\Rightarrow3+2x=15-4\)
\(\Rightarrow3+2x=11\)
\(\Rightarrow2x=11-3\)
\(\Rightarrow2x=8\)
\(\Rightarrow x=\dfrac{8}{2}\)
\(\Rightarrow x=4\)
c) \(-11-\left(19-x\right)=50\)
\(\Rightarrow19-x=-11-50\)
\(\Rightarrow19-x=-61\)
\(\Rightarrow x=61+19\)
\(\Rightarrow x=80\)
d) \(159-\left(25-x\right)=43\)
\(\Rightarrow25-x=159-43\)
\(\Rightarrow25-x=116\)
\(\Rightarrow x=25-116\)
\(\Rightarrow x=-91\)
e) \(\left(79-x\right)-43=-\left(17-52\right)\)
\(\Rightarrow\left(79-x\right)-43=52-17\)
\(\Rightarrow79-x-43=35\)
\(\Rightarrow36-x=35\)
\(\Rightarrow x=1\)
f) \(\left(7+x\right)-\left(21-13\right)=32\)
\(\Rightarrow7+x-8=32\)
\(\Rightarrow x-1=32\)
\(\Rightarrow x=32+1\)
\(\Rightarrow x=33\)
g) \(-x+20=-15+8+13\)
\(\Rightarrow-x+20=6\)
\(\Rightarrow x=20-6\)
\(\Rightarrow x=14\)
h) \(-\left(-x+13-142\right)+18=55\)
\(\Rightarrow x-13+142+18=55\)
\(\Rightarrow x+147=55\)
\(\Rightarrow x=55-147\)
\(\Rightarrow x=-92\)
Đề bài j kì vậy???
Lần đầu gặp!!
nó cho đề linh tinh, ko có công thức cho dạng này