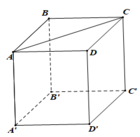
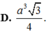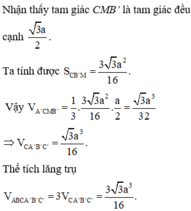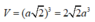Cho lăng trụ tứ giác đều ABCD.A'B'C'D' có chiều cao bằng a. Mặt phẳng ( A'BD) hợp vs mặt bên (ABB'A') một góc 60° . Tích thể tích hình lăng trụ.
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
CM
28 tháng 2 2019
Chọn A
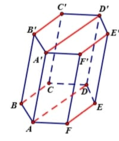
TH1: Có 3 bộ, mỗi bộ gồm 6 đường thẳng song song nhau (như hình vẽ)
Đa giác đáy của hình chóp gồm 1 đường thẳng ở nhóm 3 đường thẳng song song trên (ABCDEF) và có 1 đường thẳng ở nhóm 3 đường thẳng song song trên (A’B’C’D’E’F’)
Suy ra số đa giác đáy là C 3 1 C 3 1 .
Vậy TH1 có 3 . C 3 1 . C 3 1 . 8 = 216 hình chóp
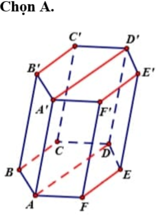
TH2: Đa giác đáy của hình chóp là tứ giác nằm trên một mặt đáy của hình lăng trụ (hình vẽ).
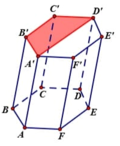
Số đa giác đáy là C 6 4 . 2
Vậy số hình chóp tạo thành ở TH2 là C 6 4 . 2 . 6 = 180 hình chóp
TH3: Có 3 bộ gồm 4 đường thẳng song song nhau (như hình vẽ)
Đa giác đáy của hình chóp gồm 1 đường thẳng có ở nhóm 2 đường chéo song song trên (ABCDEF) và 1 đường thẳng ở nhóm 2 đường chéo song song trên (A’B’C’D’E’F’)
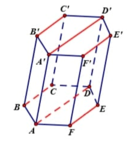
Số đa giác đáy là C 2 1 C 2 1
Vậy số hình chóp được tạo thành ở TH3 là 3 . C 2 1 . C 2 1 . 8 = 96
Do đó, số hình chóp cần tìm là 216 + 180 + 96 =492.
CM
4 tháng 6 2017
Phương pháp:
Thể tích khối lăng trụ có diện tích đáy S và chiều cao h là V = h.S
Cách giải:
Diện tích đáy lăng trụ là S = a2
Thể tích lăng trụ là V = h.S = 2a.a2 = 2a3
Chọn: D
CM
7 tháng 4 2018
Đáp án B
Hình lăng trụ tứ giác đều có tất cả các cạnh bằng nhau là hình lập phương.
Gọi a là độ dài một cạch thì tổng diện tích các mặt S = 6 a 2 => a = 4.
=> thể tích lăng trụ là V = a 3 = 4 3 = 64