Ghi giả thiết,kết luận và chứng minh :"Hai góc phụ nhau với góc thứ ba thì bằng nhau "
Ghi giả thiết,kết luận và chứng minh:"Hai góc cùng bù với một góc thứ ba thì bằng nhau".
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
6 tháng 9 2015
ĐL 1: GT: góc A + Góc C = ; góc B + Góc C =
KL:Góc A = góc B
CM: góc A+C=góc B+C=
A+C-C=B+C-C (bỏ chữ góc cho gọn nhé)
A=B(dpcm)
ĐL2: góc A + Góc C = ; góc B + Góc C =
KL:Góc A = góc B
CM: A+C=góc B+C=
A+C-C=B+C-C
A=B(dpcm)
6 tháng 9 2015
a. gt:hai góc cùng phụ
kl:hai góc bằng nhau
giai : goi hai góc a va b cùng phụ với c ta dược
a+c=90 =>a=90-c
b+c=90=>b=90-c
từ 2 điều trên suy ra a=b
b. tương tụ trên chỉ cwnf thay phụ thành bù. 90 thanh 180
17 tháng 9 2015
Kéo dài O'y' cắt Ox tại A
Vì Ox // O'x' => góc A1 = O'1 (2 góc đồng vị)
Vì Oy // O'y' => góc A1 = O1 (2 góc đồng vị)
=> góc O1 = O'1
4 tháng 2 2022
Bài 1:
| GT | \(\widehat{A}+\widehat{B}=90^0;\widehat{C}+\widehat{B}=90^0\) |
| KL | \(\widehat{A}=\widehat{C}\) |
Ta có: \(\widehat{A}+\widehat{B}=90^0\)
nên \(\widehat{A}=90^0-\widehat{B}\left(1\right)\)
Ta có: \(\widehat{C}+\widehat{B}=90^0\)
nên \(\widehat{C}=90^0-\widehat{B}\left(2\right)\)
Từ (1) và (2) suy ra \(\widehat{A}=\widehat{C}\)
PT
1
CM
30 tháng 5 2019
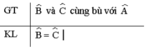
Chứng minh:
∠B bù với ∠A ⇒ ∠B + ∠A = 180o ⇒ ∠B = 180o - ∠A
∠C bù với ∠A ⇒ ∠C + ∠A = 180o ⇒ ∠C = 180o - ∠A
Vậy ∠B = ∠C.
CM
3 tháng 10 2018
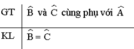
Chứng minh:
∠B phụ với ∠A ⇒ ∠B + ∠A = 90o ⇒ ∠B = 90o - ∠A
∠C phụ với ∠A ⇒ ∠C + ∠A = 90o ⇒ ∠C = 90o - ∠A
Vậy ∠B = ∠C.
TH
0
VH
1
5 tháng 10 2016
GT: x bù vs z ; y bù vs z
KL: x = y
CM: ta có x + z = 1800 (1)
y + z = 1800 (2)
từ (1) và (2) => x=y