Trên nữa đường tròn tâm O đường kính AD=2R lấy hai điểm B,C sao cho ba dây cung AB,BC,CD bằng nhau. Hai tiếp tuyến tại B và D cắt nhau ở M
a) Chứng minh O,C,M thẳng hàng
b) Tính diện tích tam giác MBD theo R
Giúp mình 🆚
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
NH
27 tháng 5 2017
Vì dây AB = BC= CD => các góc AOB = BOC = COD = 180:3 =60 .
Gọi H là đường cao kẻ từ M tới cạnh BD
Ta có OBD = ODB => OH vuông góc với BD (1)
Mà C là điểm chính giữa cung BC => CH vuông góc với BD (2)
Vì M là giao điểm của hai tiếp tuyến nên theo t/c hai tiếp tuyến cắt nhau ta có MB = MD
=> MH vuông góc với BD (3)
Từ 1 2 3 => OH //CH//MH có H chung => O,C,M thẳng hàng( mình nghĩ là đung nhưng lập luận của mình thật sự không logic)
b.Theo câu a ta tính được góc HDO = 30
SinHDO =0H/OD => OH =sin30.OD =1/2.R =R/2
Theo py ta go tính được BH = căn( R^2-(R/2)^2)=(R căn 3)/2
sin DMO = OD/MO => MO = OD/sin 30 = 2R => MH =MO-OH= 2R- R/2=3R/2
BD = 2BH =2 (Rcăn 3)/2 =căn3R
=> SMBD = (MH.BD)/2= (3R./2.căn3R)/2=(3căn3r^2)/4 (đvdt)
12 tháng 5 2023
a: góc ANM+góc ACM=180 độ
=>ANMC nội tiếp
b: Xét ΔANM vuông tại N và ΔADB vuông tại D có
góc NAM chung
=>ΔANM đồng dạng với ΔADB
=>AN/AD=AM/AB
=>AM*AD=AN*AB
CM
20 tháng 10 2017
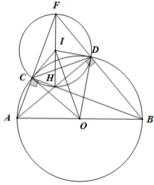
a) Vì C, D thuộc nửa đường tròn đường kính AB nên
A C B = A D B = 90 o ⇒ F C H = F D H = 90 o ⇒ F C H + F D H = 180 o
Suy ra tứ giác CHDF nội tiếp
b) Vì AH ⊥ BF, BH ⊥ AF nên H là trực tâm ∆ AFB ⇒ FH ⊥ AB
⇒ C F H = C B A ( = 90 o − C A B ) ⇒ Δ C F H ~ Δ C B A ( g . g ) ⇒ C F C B = C H C A ⇒ C F . C A = C H . C B