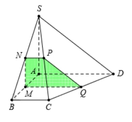
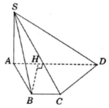
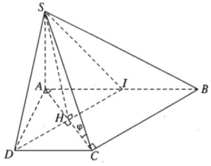
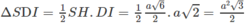Hình chóp S.ABCD có đáy là hình thang vuông ABCD vuông tại A và D, có AB = 2a, AD = DC = a, có cạnh SA vuông góc với mặt phẳng (ABCD) và SA = a
a) Chứng minh mặt phẳng (SAD) vuông góc với mặt phẳng (SDC), mặt phẳng (SAC) vuông góc với mặt phẳng (SCB)
b) Gọi \(\varphi\) là góc giữa hai mặt phẳng (SBC) và (ABCD), tính \(\tan\varphi\)
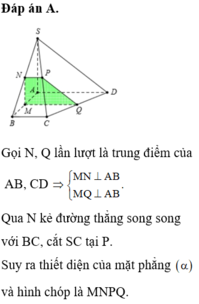
c) Gọi \(\left(\alpha\right)\) là mặt phẳng chứa SD và vuông góc với mặt phẳng (SAC). Hãy xác định \(\left(\alpha\right)\) và xác định thiết diện của hình chóp S.ABCD với \(\left(\alpha\right)\)


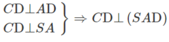
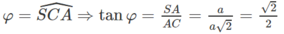
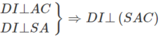
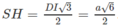 .
.