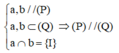Câu 1:Gọi (P) là mp đi qua M(3;-1;-5) và vuông góc với hai mp (Q):3x-2y+2z+7=0 và (R):5x-4y+3z+1=0
A.2x+y-2z+15=0 B.2x+y-2z-15=0 C.x+y+z-7=0 D.x+2y+3z+2=0
Câu 2:Tồn tại bao nhiêu mp (P) vuông góc với 2 mp (\(\alpha\)):x+y+z+1=0,(\(\beta\)):2x-y+3z-4=0 sao cho khoảng cách từ gốc tọa độ đến mp (P) bằng \(\sqrt{26}\)
A.0 B.2 C.1 D.vô số
Câu 3: Trong Oxyz cho A(3; 4; -1),B(2;0;3),C(-3;5;4).Diện tích tam giác ABC là:
A.7 B.\(\dfrac{\sqrt{1562}}{2}\) C.\(\dfrac{\sqrt{379}}{2}\) D.\(\dfrac{\sqrt{29}}{2}\)
Câu 4:Cho hai đt (d1):\(\dfrac{x-1}{2}=\dfrac{y-2}{3}=\dfrac{z-3}{4}\)và (d2)\(\dfrac{x-3}{4}=\dfrac{y-5}{6}=\dfrac{z-7}{8}\).Mệnh đề nào dưới đây đúng?
A.(d1)\(\perp\)(d2) B.(d1)\(\equiv\)(d2) C.(d1)//(d2) D.(d1) và (d2) chéo nhau