Bài 1: Có bao nhiêu cách viết phân số \(\dfrac{1}{5}\) dưới dạng tổng của hai phân số \(\dfrac{1}{a}+\dfrac{1}{b}\) với 0 < a < b?
Bài 2: Tìm số tự nhiên có hai chữ số sao cho tỉ số giữa số đó với tổng các chữ số của nó là lớn nhất.
Bài 3: Có thể tìm được hai chữ số a và b sao cho phân số \(\dfrac{a}{b}\) bằng số thập phân a,b hay không?
Bài 4: Một công nhân có thể hoàn thành công việc được giao trong 3 giờ 20 phút. Một công nhân khác có thể hoàn thành công việc đó trong 4 giờ 10 phút. Nếu cùng làm, cả hai làm được 72 sản phẩm. Hỏi mỗi người làm bao nhiêu sản phẩm?
Bài 5: Cho hai điểm M và N nằm cùng phía đối với A, nằm cùng phía đối với B. Điểm M nằm giữa A và B. Biết AB = 5cm ; AM = 3cm ; BN = 1cm. Chứng tỏ rằng:
a, Bốn điểm A , B , M , N thẳng hàng.
b, Điểm N là trung điểm của đoạn thẳng MB.
c, Vẽ đường tròn tâm N đi qua B và đường tròn tâm A đi qua N, chúng cắt nhau tại C. Tính chu vi của tam giác CAN

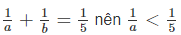 Suy ra a > 5 (1)
Suy ra a > 5 (1)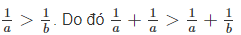
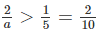 , suy ra a < 10 (2)
, suy ra a < 10 (2)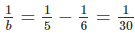 nên b = 30
nên b = 30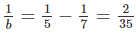 suy ra b = 17,5 (loại)
suy ra b = 17,5 (loại)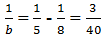 suy ra b ≈ 13,3 (loại)
suy ra b ≈ 13,3 (loại)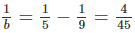 suy ra b = 11,25 (loại)
suy ra b = 11,25 (loại)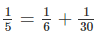
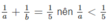 Suy ra a > 5 (1)
Suy ra a > 5 (1)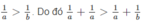
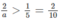 , suy ra a < 10 (2)
, suy ra a < 10 (2)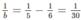 nên b = 30
nên b = 30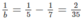 suy ra b = 17,5 (loại)
suy ra b = 17,5 (loại)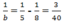 suy ra b ≈ 13,3 (loại)
suy ra b ≈ 13,3 (loại)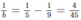 suy ra b = 11,25 (loại)
suy ra b = 11,25 (loại)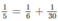
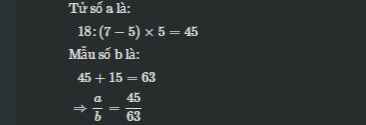

Bài 1: Giải:
Ta có:
\(\dfrac{1}{a}+\dfrac{1}{b}=\dfrac{1}{5}\Leftrightarrow\dfrac{1}{a}< \dfrac{1}{5}\Leftrightarrow a>5\left(1\right)\)
Ta lại có:
\(0< a< b\Leftrightarrow\dfrac{1}{a}>\dfrac{1}{b}\Leftrightarrow\dfrac{1}{a}+\dfrac{1}{a}>\dfrac{1}{a}+\dfrac{1}{b}\)
Hay \(\dfrac{2}{a}>\dfrac{1}{5}\Leftrightarrow\dfrac{2}{a}>\dfrac{2}{10}\Leftrightarrow a< 10\left(2\right)\)
Kết hợp \(\left(1\right)\) và \(\left(2\right)\) \(\Rightarrow a\in\left\{6;7;8;9\right\}\)
Xét từng trường hợp chỉ có:
\(a=6\Leftrightarrow\dfrac{1}{b}=\dfrac{1}{5}-\dfrac{1}{6}=\dfrac{1}{30}\Leftrightarrow b=30\) là thỏa mãn
Vậy chỉ có một cách viết duy nhất là \(\dfrac{1}{5}=\dfrac{1}{6}+\dfrac{1}{30}\)
Bài 2: Giải:
Gọi số tự nhiên hai chữ số có tỉ số giữa số đó với tổng các chữ số của nó là lớn nhất là \(\dfrac{\overline{ab}}{a+b}\)
Đặt \(k=\dfrac{\overline{ab}}{a+b}.\) Ta có:
\(k=\dfrac{\overline{ab}}{a+b}=\dfrac{10a+b}{a+b}\ge\dfrac{10a+10b}{a+b}=10\)
\(\Leftrightarrow k=10\Leftrightarrow b=10b\Leftrightarrow b=0\)
Vậy \(k_{\text{lớn nhất}}=10\) ứng với các số \(10;20;30;...;90\)
Bài 3: Giải:
Giả sử ta tìm được hai chữ số \(a\) và \(b\) sao cho \(\dfrac{a}{b}=a,b\)
Rõ ràng ta thấy: \(a,b>a\left(b\ne0\right)\)
Ta có: \(\dfrac{a}{b}=a.\dfrac{1}{b}\) Mà \(\dfrac{1}{b}\le1\) nên \(a.\dfrac{1}{b}\le a\)
Hay \(\dfrac{a}{b}\le a\Leftrightarrow\dfrac{a}{b}< a,b\)
Vậy không tìm được hai chữ số \(a,b\) thỏa mãn đề bài.