Cho đoạn thẳng AB. Vẽ các cung tâm A và B có cùng bán kính sao cho chúng cắt nhau tại C và D. Chứng minh rằng CD là đường trung trục của AB ?
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
CM
20 tháng 6 2019
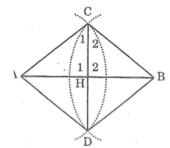
Gọi H là giao điểm của AB và CD
Nối AC, AD,BC,BD
Xét ΔACD và ΔBCD, ta có:
AC = BC
(bán kính hai cung tròn bằng nhau)
AD = BD
CD cạnh chung
Suy ra: ΔACD = ΔBCD(c.c.c)
Suy ra: ∠C1 = ∠C2 (hai góc tương ứng)
Xét hai tam giác AHC và BHC. Ta có:
AC = BC (bán kính hai cung tròn bằng nhau)
∠C1 = ∠C2 (chứng minh trên)
CH cạnh chung
Suy ra: ΔAHC = ΔBHC(c.g.c)
Suy ra: AH = BH (hai cạnh tương ứng) (1)
Ta có : ∠H1 = ∠H2 (hai góc tương ứng)
∠H1 + ∠H2 =180° (hai góc kề bù)
Suy ra: ∠H1 = ∠H2 = 90o ⇒ CD ⊥ AB (2)
Từ (1) và (2) suy ra CD là đường trung trực của AB
LA
24 tháng 2 2018
Hướng dẫn, tự vẽ hình:
Trung tâm A và B cùng bán kính
=> CA = CB DA = DB
Hai điểm C D cách đều 2 điểm A B nên CD là đường trung trực của AB.
24 tháng 2 2018
Cung tâm A và cung tâm B có cùng bán kính
\(\Rightarrow\)CA = CB
Và DA = DB
Hai điểm C và D cách đều 2 điểm A và B nên CD là đường trung trực của AB ( đpcm )
27 tháng 2 2019
Lời giải:
Bài 1:
Gọi H là giao điểm của AB và CD
Nối AC, AD,BC,BD
Xét ΔACD và ΔBCD, ta có:
AC = BC
(bán kính hai cung tròn bằng nhau)
AD = BD
CD cạnh chung
Suy ra: ΔACD= ΔBCD(c.c.c)
Suy ra: ∠C2 =∠C2 (hai góc tương ứng)
Xét hai tam giác AHC và BHC. Ta có:
AC = BC (bán kính hai cung tròn bằng nhau)
∠C2 =∠C2 (chứng minh trên)
CH cạnh chung
Suy ra: ΔAHC= ΔBHC(c.g.c)
Suy ra: AH = BH (hai cạnh tương ứng) (1)
Ta có : ∠H1 =∠H2 (hai góc tương ứng)
∠H1 + ∠H2 =180° (hai góc kề bù)
Suy ra: ∠H1 =∠H2 =90° => CD ⊥ AB (2)
Từ (1) và (2) suy ra CD là đường trung trực của AB
27 tháng 2 2019
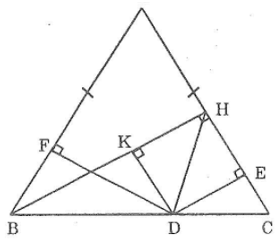
bài 2
Kẻ DK ⊥ BH
Ta có: BH ⊥AC(gt)
Suy ra: DK // AC (hai đường thẳng cùng vuông góc với đường thẳng thứ ba thì song song)
=> ∠KDB =C (hai góc đồng vị)
VìΔABC cân tại A nên ∠B =∠C (tính chất tam giác cân)
Suy ra: ∠KDB =B
Xét hai tam giác vuông BFD và DKB, ta có:
∠BFD =∠DKB
BD cạnh huyền chung
∠FBD =∠KDB (chứng minh trên)
Suy ra:ΔBFD=ΔDKB(cạnh huyền góc nhọn)
=> DF = BK (hai cạnh tương ứng)(1)
Nối DH. XétΔDEHvàΔDKH, ta có:
∠DEH =∠DKH =90°
DH cạnh huyền chung
∠EHD =∠KDH (hai góc so le trong)
Suy ra:ΔDEH=ΔDKH( cạnh huyền , góc nhọn)
Suy ra: DE = HK ( hai cạnh tương ứng) (2)
Mặt khác : BH = BK + KH (3)
Từ (1), (2) và (3) suy ra: DF = DE = BH
31 tháng 1 2021
Bạn chỉ cần viết lại khúc từ cung tròn tâm A đến ở C và D rồi suy ra AC=AB=AD=BD=BC là đc nhé còn lại tự giải
A
16 tháng 11 2018
ta có : mình vẽ ko đúng lắm nhé
xét tam giác acm và tam giác bcm
có:am=bm(cùng bằng bán kính)
chung cm
bc=ca(m là trung điểm của ab)
vậy tam giac acm băng tam giác bcm (c.c.c)
vậy góc cma=góc cmb(2 góc tương ứng)
vì acb=180o mà cm nằm giữa ca và cb
vậy góc cma= góc cmb=góc acb/2=1800/2=90o
vậy góc cma và cmb vuông
vậy cm vuông góc với ab
CM
4 tháng 2 2019
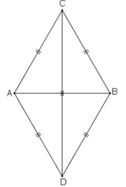
Xét ΔABC và ΔABD, ta có:
AC = AD (bằng bán kính đường tròn (A))
Ab cạnh chung
BC = BD (bằng bán kính đường tròn (B))
Suy ra: ΔABC = ΔABD (c.c.c)
CM
21 tháng 3 2019
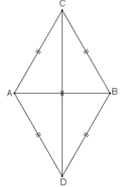
Xét ΔACD và ΔBCD, ta có:
AC = BC (= AB)
CD cạnh chung
AD = BD (= AB)
Suy ra: ΔACD = ΔBCD(c.c.c)
27 tháng 8 2023
a) Xét tam giác NMA và NMB có:
\(MA=MB\left(gt\right)\)
\(NM\) là cạnh chung.
\(NA=NB\) (đường tròn tâm A và B cùng bán kính cắt nhau)
\(\Rightarrow\Delta NMA=\Delta NMB\left(c.c.c\right)\) (1)
b) Vì \(\widehat{NMA}=\widehat{NMB}\) (từ 1) và 2 góc trên là 2 góc kề bù nên \(\widehat{NMA}=\widehat{NMB}=90^o\)
Vậy \(NM\perp AB\)
c) \(NA=NB\) (từ 1)
\(BM=\dfrac{AB}{2}=\dfrac{12}{2}=6\left(cm\right)\)
Chu vi tam giác NMB:
\(10+8+6=24\left(cm\right)\)
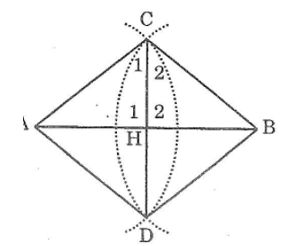
Xét hai tam giác ACD và BCD có:
AC = BC (gt)
AD = BD (gt)
CD: cạnh chung
Vậy: \(\Delta ACD=\Delta BCD\left(c-c-c\right)\)
Suy ra: \(\widehat{C_1}=\widehat{C_2}\) (hai góc tương ứng)
Xét hai tam giác ACH và BCH có:
AC = BC (gt)
\(\widehat{C_1}=\widehat{C_2}\) (cmt)
CH: cạnh chung
Vậy: \(\Delta ACH=\Delta BCH\left(c-g-c\right)\)
Suy ra: \(\widehat{H_1}=\widehat{H_2}\), HA = HB
Mà \(\widehat{H_1}+\widehat{H_2}=180^o\)
Nên \(\widehat{H_1}=\widehat{H_2}\) = 90o
Do đó: \(CH\perp AB\)
Vì \(CD\perp AB\)và HA = HB nên CD là đường trung trực của AB.