Đường trung trực d của đoạn thẳng AB chia mặt phẳng thành hai phần (không kể đường thẳng d) : phần chứa điểm A kí hiệu là \(P_A\), phần chứa điểm B kí hiệu là \(P_B\) (h.21)
a) Gọi M là một điểm \(P_A\). Chứng minh rằng MA < MB
b) Gọi N là một điểm \(P_B\). Chứng minh rằng NB < NA
c) Gọi K là một điểm sao cho KA < KB. Hỏi rằng K nằm ở đâu : trong \(P_A,P_B\) hay trên d...
Đọc tiếp
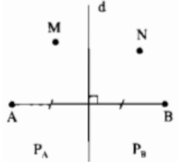
Đường trung trực d của đoạn thẳng AB chia mặt phẳng thành hai phần (không kể đường thẳng d) : phần chứa điểm A kí hiệu là \(P_A\), phần chứa điểm B kí hiệu là \(P_B\) (h.21)
a) Gọi M là một điểm \(P_A\). Chứng minh rằng MA < MB
b) Gọi N là một điểm \(P_B\). Chứng minh rằng NB < NA
c) Gọi K là một điểm sao cho KA < KB. Hỏi rằng K nằm ở đâu : trong \(P_A,P_B\) hay trên d ?
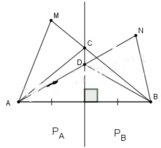
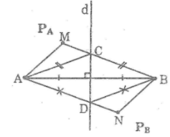
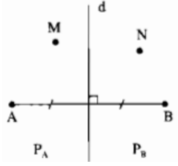
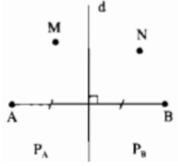
a. Gọi C là giao điểm của MB với đường thẳng d.
Ta có: MB=MC+CB
mà CA=CB(tính chất đường trung trực)
Suy ra: MB=MC+CA(1)
Trong ΔMAC ta có:
MA<MC+CA(bất đẳng thức tam giác)(2)
Từ (1) và (2) suy ra: MA<MB
b.Gọi D là giao điểm của NA với đường thẳng d.
Ta có: NA=ND+DA
mà DA=DB(tính chất đường trung trực)
Suy ra: NA=ND+DB(3)
Trong ΔNDB, ta có:
NB<ND+DB (bất đẳng thức tam giác) (4)
Từ (3) và (4) suy ra: NA>NB
c) Theo phần a và b; với điểm H bất kì ta có:
+ Nếu H nằm trong phần PA thì HA < HB.
+ Nếu H nằm trong phần PB thì HB < HA.
+ Nếu H nằm trên đường thẳng d thì HA = HB (tính chất đường trung trực)
Do đó, để KA < KB thì K nằm trong phần PA.